Question Number 106465 by mohammad17 last updated on 05/Aug/20

Answered by Dwaipayan Shikari last updated on 05/Aug/20
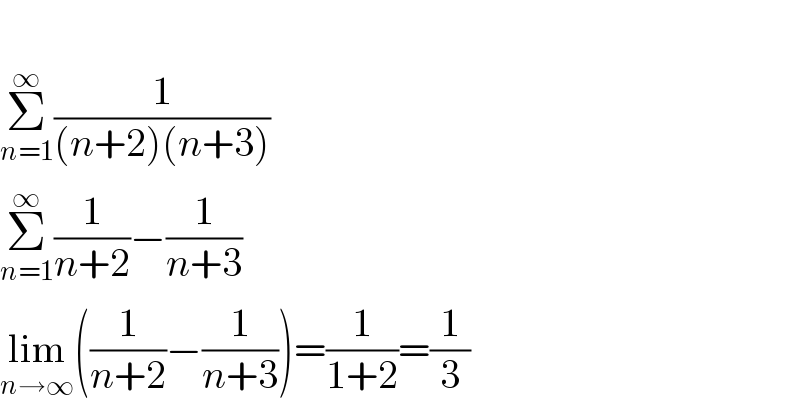
$$ \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}+\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{3}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{n}+\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by mohammad17 last updated on 05/Aug/20
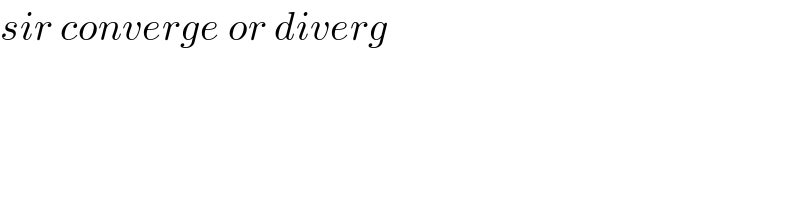
$${sir}\:{converge}\:{or}\:{diverg} \\ $$
Commented by Dwaipayan Shikari last updated on 05/Aug/20

$${Converges} \\ $$
