Question Number 106655 by Algoritm last updated on 06/Aug/20
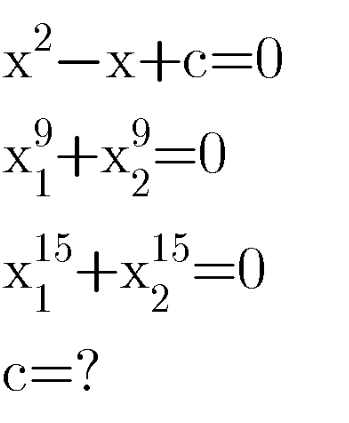
Commented by prakash jain last updated on 06/Aug/20

$${x}_{\mathrm{1}} ={kx}_{\mathrm{2}} \\ $$$${k}^{\mathrm{9}} =−\mathrm{1}\Rightarrow{k}=−\mathrm{1}\left({e}^{{i}\mathrm{2}\pi{m}/\mathrm{9}} \right)\:\:\left({m}=\mathrm{0}..\mathrm{8}\right)\:\left({I}\right) \\ $$$${k}^{\mathrm{15}} =−\mathrm{1} \\ $$$${only}\:{applicable}\:{solution}\:{from}\:\left({I}\right) \\ $$$${for}\:{k}\:{are} \\ $$$${k}=−\mathrm{1},−{e}^{{i}\mathrm{2}\pi/\mathrm{3}} ,−{e}^{{i}\mathrm{4}\pi/\mathrm{3}} \\ $$$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} =\mathrm{1} \\ $$$${x}_{\mathrm{1}} \left(\mathrm{1}+{k}\right)=\mathrm{1}\Rightarrow{x}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}+{k}} \\ $$$${k}=−\mathrm{1}\:\mathrm{is}\:\mathrm{invalid} \\ $$$$\Rightarrow{k}=−{e}^{\mathrm{2}\pi{i}/\mathrm{3}} ,−{e}^{\mathrm{4}\pi{i}/\mathrm{3}} \\ $$$${c}={x}_{\mathrm{1}} {x}_{\mathrm{2}} ={kx}_{\mathrm{1}} ^{\mathrm{2}} =\frac{{k}}{\left(\mathrm{1}+{k}\right)^{\mathrm{2}} } \\ $$$${where}\:{k}=−{e}^{\mathrm{2}\pi{i}/\mathrm{3}} ,−{e}^{\mathrm{4}\pi{i}/\mathrm{3}} \\ $$
