Question-106663

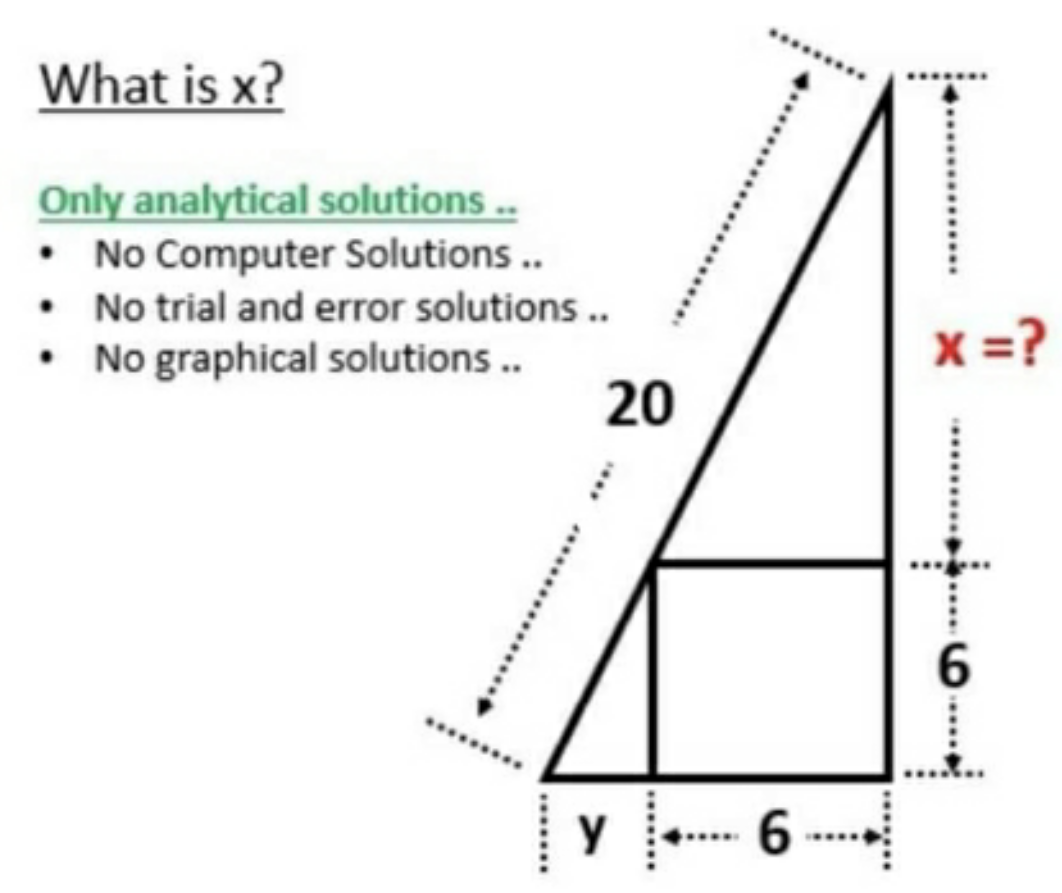
Question Number 106663 by I want to learn more last updated on 06/Aug/20

Answered by Her_Majesty last updated on 06/Aug/20

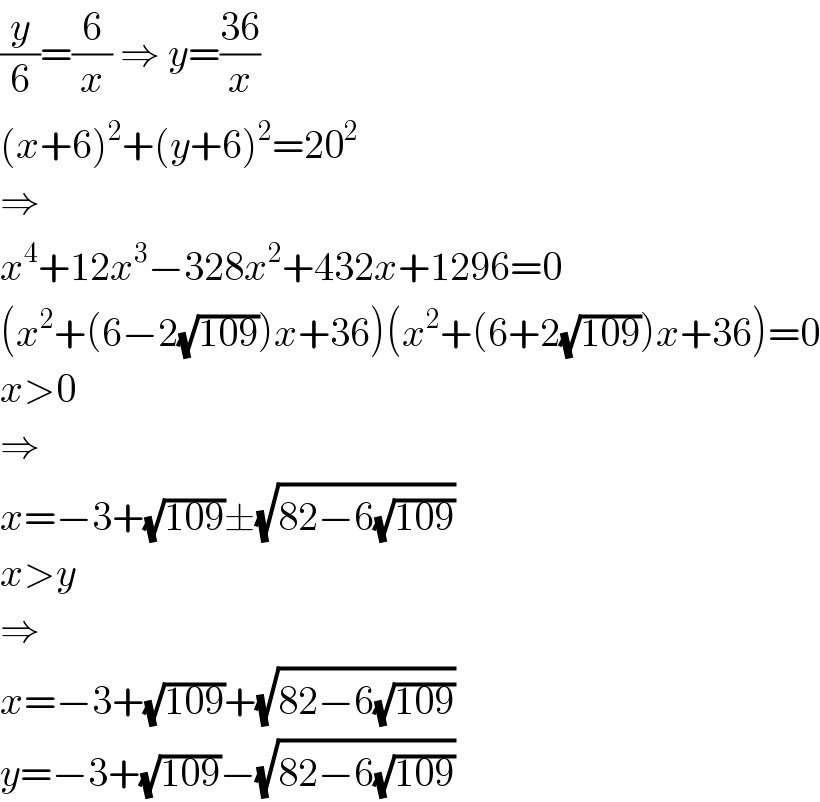
(y/6)=(6/x) ⇒ y=((36)/x) (x+6)^2 +(y+6)^2 =20^2 ⇒ x^4 +12x^3 −328x^2 +432x+1296=0 (x^2 +(6−2(√(109)))x+36)(x^2 +(6+2(√(109)))x+36)=0 x>0 ⇒ x=−3+(√(109))±(√(82−6(√(109)))) x>y ⇒ x=−3+(√(109))+(√(82−6(√(109)))) y=−3+(√(109))−(√(82−6(√(109))))

$$\frac{{y}}{\mathrm{6}}=\frac{\mathrm{6}}{{x}}\:\Rightarrow\:{y}=\frac{\mathrm{36}}{{x}} \\ $$$$\left({x}+\mathrm{6}\right)^{\mathrm{2}} +\left({y}+\mathrm{6}\right)^{\mathrm{2}} =\mathrm{20}^{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${x}^{\mathrm{4}} +\mathrm{12}{x}^{\mathrm{3}} −\mathrm{328}{x}^{\mathrm{2}} +\mathrm{432}{x}+\mathrm{1296}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} +\left(\mathrm{6}−\mathrm{2}\sqrt{\mathrm{109}}\right){x}+\mathrm{36}\right)\left({x}^{\mathrm{2}} +\left(\mathrm{6}+\mathrm{2}\sqrt{\mathrm{109}}\right){x}+\mathrm{36}\right)=\mathrm{0} \\ $$$${x}>\mathrm{0} \\ $$$$\Rightarrow \\ $$$${x}=−\mathrm{3}+\sqrt{\mathrm{109}}\pm\sqrt{\mathrm{82}−\mathrm{6}\sqrt{\mathrm{109}}} \\ $$$${x}>{y} \\ $$$$\Rightarrow \\ $$$${x}=−\mathrm{3}+\sqrt{\mathrm{109}}+\sqrt{\mathrm{82}−\mathrm{6}\sqrt{\mathrm{109}}} \\ $$$${y}=−\mathrm{3}+\sqrt{\mathrm{109}}−\sqrt{\mathrm{82}−\mathrm{6}\sqrt{\mathrm{109}}} \\ $$

Answered by Aziztisffola last updated on 06/Aug/20

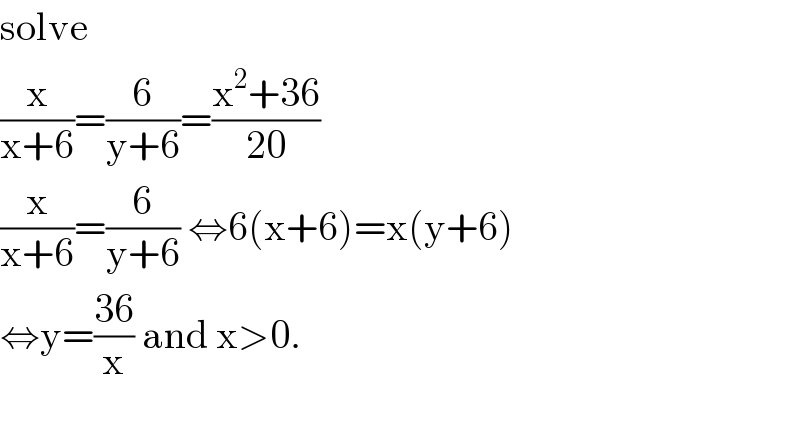
solve (x/(x+6))=(6/(y+6))=((x^2 +36)/(20)) (x/(x+6))=(6/(y+6)) ⇔6(x+6)=x(y+6) ⇔y=((36)/x) and x>0.

$$\mathrm{solve} \\ $$$$\frac{\mathrm{x}}{\mathrm{x}+\mathrm{6}}=\frac{\mathrm{6}}{\mathrm{y}+\mathrm{6}}=\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{36}}{\mathrm{20}} \\ $$$$\frac{\mathrm{x}}{\mathrm{x}+\mathrm{6}}=\frac{\mathrm{6}}{\mathrm{y}+\mathrm{6}}\:\Leftrightarrow\mathrm{6}\left(\mathrm{x}+\mathrm{6}\right)=\mathrm{x}\left(\mathrm{y}+\mathrm{6}\right) \\ $$$$\Leftrightarrow\mathrm{y}=\frac{\mathrm{36}}{\mathrm{x}}\:\mathrm{and}\:\mathrm{x}>\mathrm{0}. \\ $$$$ \\ $$

Commented by prakash jain last updated on 06/Aug/20

Use + button at top to add a new question

$$\mathrm{Use}\:+\:\mathrm{button}\:\mathrm{at}\:\mathrm{top}\:\mathrm{to}\:\mathrm{add}\:\mathrm{a}\:\mathrm{new} \\ $$$$\mathrm{question} \\ $$

Commented by Aziztisffola last updated on 06/Aug/20

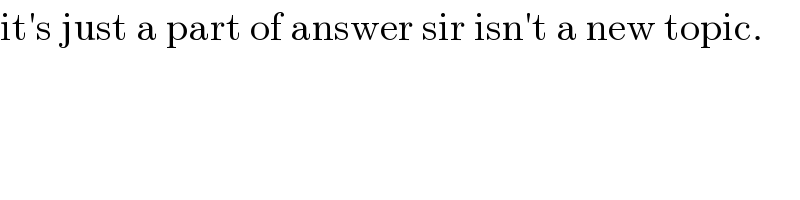
it′s just a part of answer sir isn′t a new topic.

$$\mathrm{it}'\mathrm{s}\:\mathrm{just}\:\mathrm{a}\:\mathrm{part}\:\mathrm{of}\:\mathrm{answer}\:\mathrm{sir}\:\mathrm{isn}'\mathrm{t}\:\mathrm{a}\:\mathrm{new}\:\mathrm{topic}. \\ $$

Commented by prakash jain last updated on 06/Aug/20

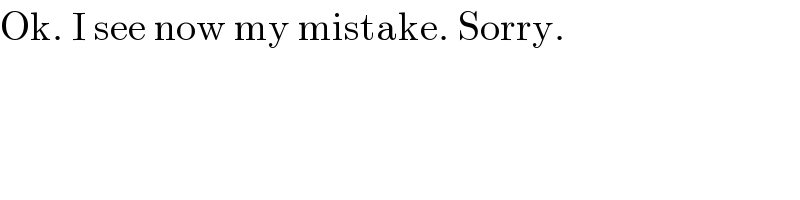
$$\mathrm{Ok}.\:\mathrm{I}\:\mathrm{see}\:\mathrm{now}\:\mathrm{my}\:\mathrm{mistake}.\:\mathrm{Sorry}. \\ $$

Commented by Aziztisffola last updated on 06/Aug/20

$$\:\mathrm{no}\:\mathrm{problem}\:\mathrm{sir} \\ $$

Commented by I want to learn more last updated on 06/Aug/20

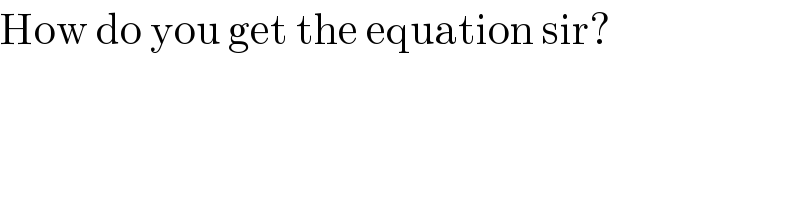
$$\mathrm{How}\:\mathrm{do}\:\mathrm{you}\:\mathrm{get}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{sir}? \\ $$

Commented by Her_Majesty last updated on 06/Aug/20

$${but}\:{you}\:{see}\:{I}\:{found}\:{a}\:{positive}\:{solution}? \\ $$$${so}\:{where}'{s}\:{the}\:{error}?\:{one}\:{of}\:{us}\:{must}\:{be} \\ $$$${wrong}\:{at}\:{least}… \\ $$

Commented by Aziztisffola last updated on 06/Aug/20

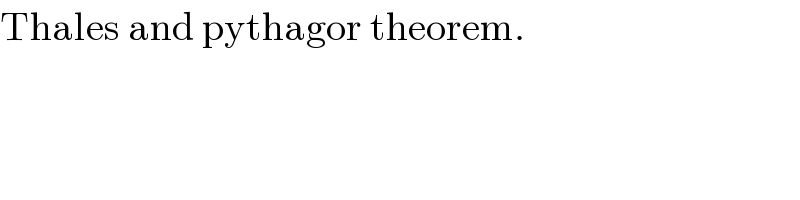
$$\mathrm{Thales}\:\mathrm{and}\:\mathrm{pythagor}\:\mathrm{theorem}. \\ $$

Commented by Her_Majesty last updated on 06/Aug/20

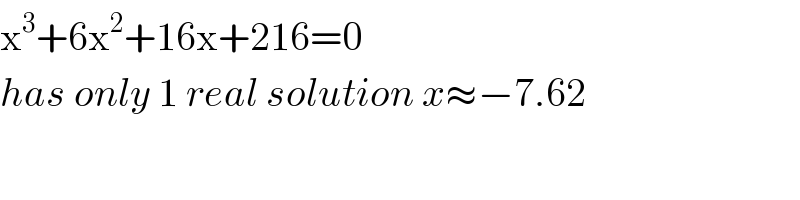
x^3 +6x^2 +16x+216=0 has only 1 real solution x≈−7.62

$$\mathrm{x}^{\mathrm{3}} +\mathrm{6x}^{\mathrm{2}} +\mathrm{16x}+\mathrm{216}=\mathrm{0} \\ $$$${has}\:{only}\:\mathrm{1}\:{real}\:{solution}\:{x}\approx−\mathrm{7}.\mathrm{62} \\ $$

Commented by Aziztisffola last updated on 06/Aug/20

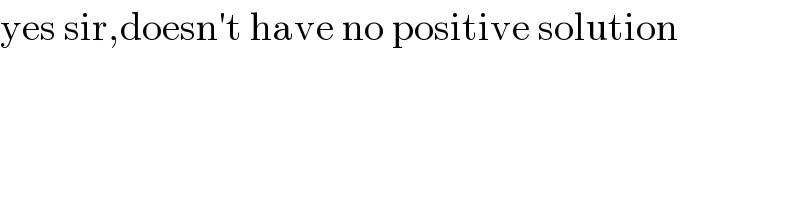
yes sir,doesn′t have no positive solution

$$\mathrm{yes}\:\mathrm{sir},\mathrm{doesn}'\mathrm{t}\:\mathrm{have}\:\mathrm{no}\:\mathrm{positive}\:\mathrm{solution} \\ $$

Commented by Aziztisffola last updated on 11/Aug/20

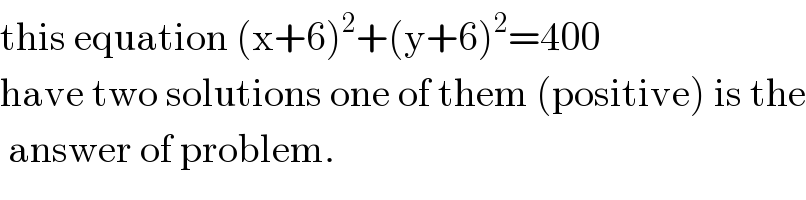
this equation (x+6)^2 +(y+6)^2 =400 have two solutions one of them (positive) is the answer of problem.

$$\mathrm{this}\:\mathrm{equation}\:\left(\mathrm{x}+\mathrm{6}\right)^{\mathrm{2}} +\left(\mathrm{y}+\mathrm{6}\right)^{\mathrm{2}} =\mathrm{400} \\ $$$$\mathrm{have}\:\mathrm{two}\:\mathrm{solutions}\:\mathrm{one}\:\mathrm{of}\:\mathrm{them}\:\left(\mathrm{positive}\right)\:\mathrm{is}\:\mathrm{the} \\ $$$$\:\mathrm{answer}\:\mathrm{of}\:\mathrm{problem}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply