Question Number 106677 by mohammad17 last updated on 06/Aug/20
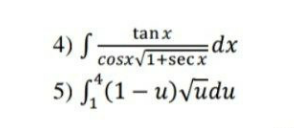
Answered by Dwaipayan Shikari last updated on 06/Aug/20
![5)∫_1 ^4 (1−u)(√u)du ∫_1 ^4 (√u)−u^(3/2) du [(2/3)u^(3/2) −(2/5)u^(5/2) ]_1 ^4 =((16)/3)−(2/3)−((64)/5)+(2/5)=((14)/3)−((62)/5)=((−116)/(15))](https://www.tinkutara.com/question/Q106680.png)
$$\left.\mathrm{5}\right)\int_{\mathrm{1}} ^{\mathrm{4}} \left(\mathrm{1}−{u}\right)\sqrt{{u}}{du} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{4}} \sqrt{{u}}−{u}^{\frac{\mathrm{3}}{\mathrm{2}}} {du} \\ $$$$\left[\frac{\mathrm{2}}{\mathrm{3}}{u}^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{2}}{\mathrm{5}}{u}^{\frac{\mathrm{5}}{\mathrm{2}}} \right]_{\mathrm{1}} ^{\mathrm{4}} =\frac{\mathrm{16}}{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{64}}{\mathrm{5}}+\frac{\mathrm{2}}{\mathrm{5}}=\frac{\mathrm{14}}{\mathrm{3}}−\frac{\mathrm{62}}{\mathrm{5}}=\frac{−\mathrm{116}}{\mathrm{15}} \\ $$
Commented by mohammad17 last updated on 06/Aug/20
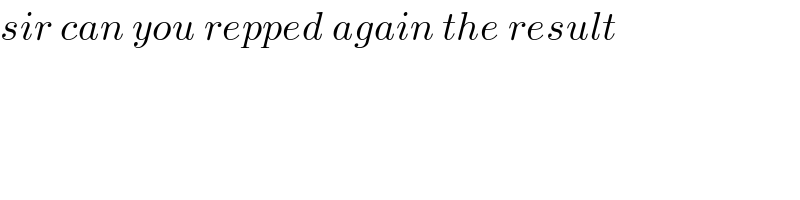
$${sir}\:{can}\:{you}\:{repped}\:{again}\:{the}\:{result} \\ $$
Commented by Her_Majesty last updated on 06/Aug/20

$${result}\:{is}\:−\frac{\mathrm{116}}{\mathrm{15}} \\ $$
Commented by mohammad17 last updated on 06/Aug/20

$${thank}\:{you}\:{sir} \\ $$
Answered by Dwaipayan Shikari last updated on 06/Aug/20
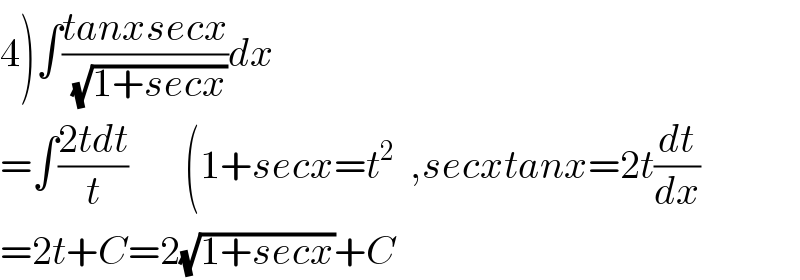
$$\left.\mathrm{4}\right)\int\frac{{tanxsecx}}{\:\sqrt{\mathrm{1}+{secx}}}{dx} \\ $$$$=\int\frac{\mathrm{2}{tdt}}{{t}}\:\:\:\:\:\:\:\left(\mathrm{1}+{secx}={t}^{\mathrm{2}} \:\:,{secxtanx}=\mathrm{2}{t}\frac{{dt}}{{dx}}\right. \\ $$$$=\mathrm{2}{t}+{C}=\mathrm{2}\sqrt{\mathrm{1}+{secx}}+{C} \\ $$
Answered by som(math1967) last updated on 06/Aug/20
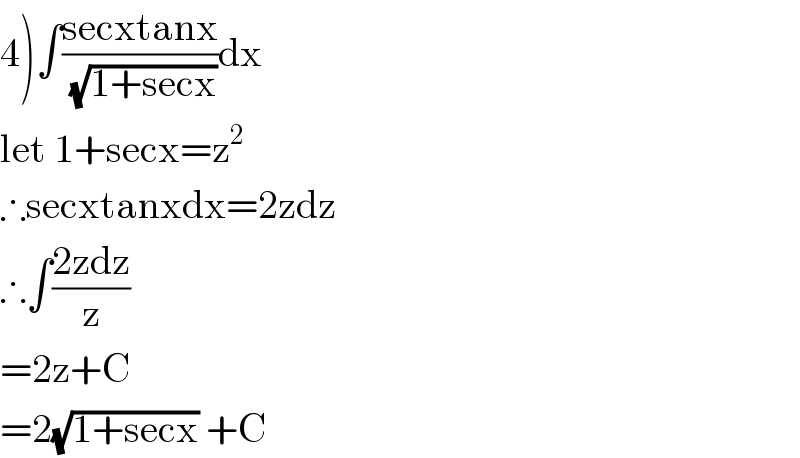
$$\left.\mathrm{4}\right)\int\frac{\mathrm{secxtanx}}{\:\sqrt{\mathrm{1}+\mathrm{secx}}}\mathrm{dx} \\ $$$$\mathrm{let}\:\mathrm{1}+\mathrm{secx}=\mathrm{z}^{\mathrm{2}} \\ $$$$\therefore\mathrm{secxtanxdx}=\mathrm{2zdz} \\ $$$$\therefore\int\frac{\mathrm{2zdz}}{\mathrm{z}} \\ $$$$=\mathrm{2z}+\mathrm{C} \\ $$$$=\mathrm{2}\sqrt{\mathrm{1}+\mathrm{secx}}\:+\mathrm{C} \\ $$
