Menu Close

Question-106694

Tinku Tara 0 Comments
Pin




Question Number 106694 by 175mohamed last updated on 06/Aug/20
Answered by bobhans last updated on 06/Aug/20
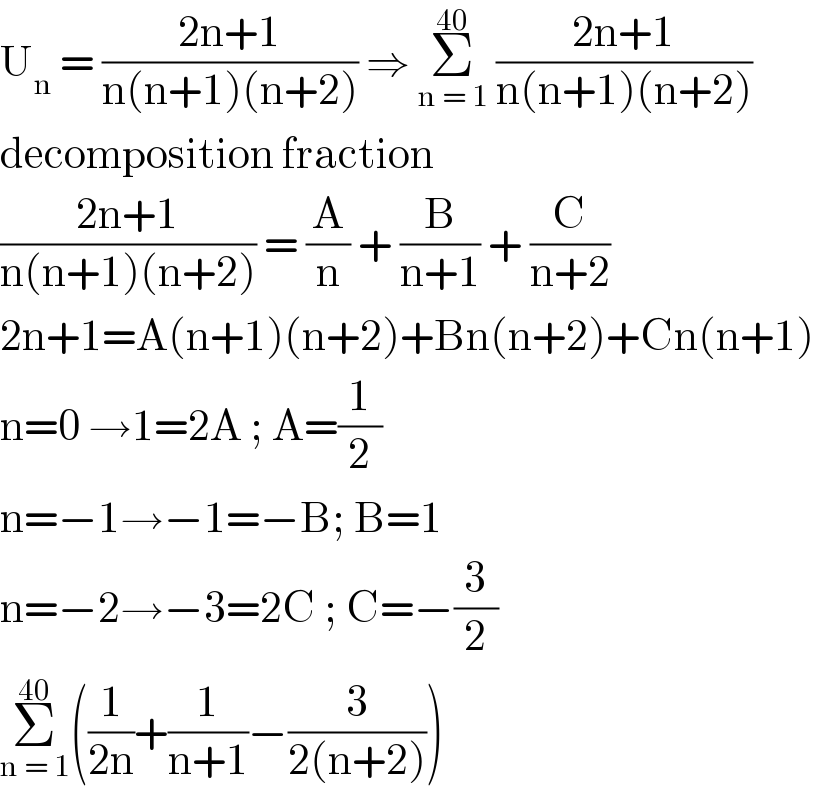
U_n = ((2n+1)/(n(n+1)(n+2))) ⇒ Σ_(n = 1) ^(40) ((2n+1)/(n(n+1)(n+2))) decomposition fraction ((2n+1)/(n(n+1)(n+2))) = (A/n) + (B/(n+1)) + (C/(n+2)) 2n+1=A(n+1)(n+2)+Bn(n+2)+Cn(n+1) n=0 →1=2A ; A=(1/2) n=−1→−1=−B; B=1 n=−2→−3=2C ; C=−(3/2) Σ_(n = 1) ^(40) ((1/(2n))+(1/(n+1))−(3/(2(n+2))))
$$\mathrm{U}_{\mathrm{n}} \:=\:\frac{\mathrm{2n}+\mathrm{1}}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)}\:\Rightarrow\:\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\mathrm{40}} {\sum}}\:\frac{\mathrm{2n}+\mathrm{1}}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)} \\ $$$$\mathrm{decomposition}\:\mathrm{fraction}\: \\ $$$$\frac{\mathrm{2n}+\mathrm{1}}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)}\:=\:\frac{\mathrm{A}}{\mathrm{n}}\:+\:\frac{\mathrm{B}}{\mathrm{n}+\mathrm{1}}\:+\:\frac{\mathrm{C}}{\mathrm{n}+\mathrm{2}} \\ $$$$\mathrm{2n}+\mathrm{1}=\mathrm{A}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)+\mathrm{Bn}\left(\mathrm{n}+\mathrm{2}\right)+\mathrm{Cn}\left(\mathrm{n}+\mathrm{1}\right) \\ $$$$\mathrm{n}=\mathrm{0}\:\rightarrow\mathrm{1}=\mathrm{2A}\:;\:\mathrm{A}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{n}=−\mathrm{1}\rightarrow−\mathrm{1}=−\mathrm{B};\:\mathrm{B}=\mathrm{1} \\ $$$$\mathrm{n}=−\mathrm{2}\rightarrow−\mathrm{3}=\mathrm{2C}\:;\:\mathrm{C}=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\mathrm{40}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2n}}+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{3}}{\mathrm{2}\left(\mathrm{n}+\mathrm{2}\right)}\right)\: \\ $$
Answered by Dwaipayan Shikari last updated on 06/Aug/20
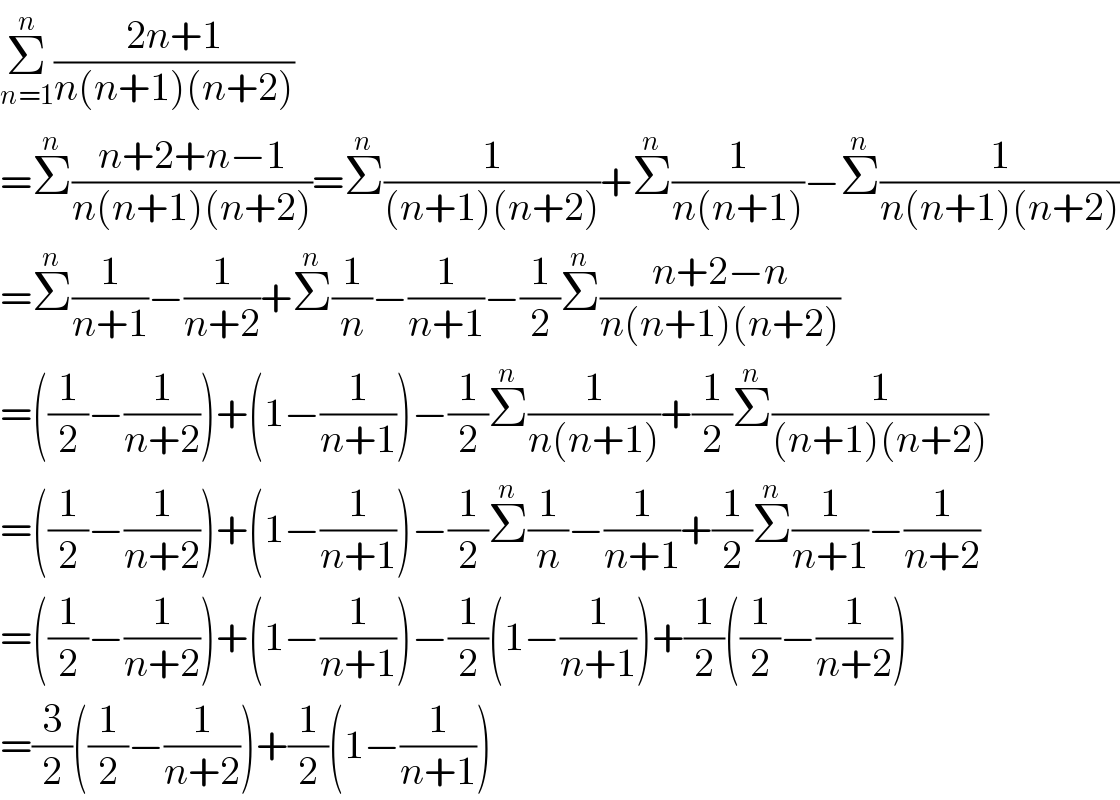
Σ_(n=1) ^n ((2n+1)/(n(n+1)(n+2))) =Σ^n ((n+2+n−1)/(n(n+1)(n+2)))=Σ^n (1/((n+1)(n+2)))+Σ^n (1/(n(n+1)))−Σ^n (1/(n(n+1)(n+2))) =Σ^n (1/(n+1))−(1/(n+2))+Σ^n (1/n)−(1/(n+1))−(1/2)Σ^n ((n+2−n)/(n(n+1)(n+2))) =((1/2)−(1/(n+2)))+(1−(1/(n+1)))−(1/2)Σ^n (1/(n(n+1)))+(1/2)Σ^n (1/((n+1)(n+2))) =((1/2)−(1/(n+2)))+(1−(1/(n+1)))−(1/2)Σ^n (1/n)−(1/(n+1))+(1/2)Σ^n (1/(n+1))−(1/(n+2)) =((1/2)−(1/(n+2)))+(1−(1/(n+1)))−(1/2)(1−(1/(n+1)))+(1/2)((1/2)−(1/(n+2))) =(3/2)((1/2)−(1/(n+2)))+(1/2)(1−(1/(n+1)))
$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{2}{n}+\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)} \\ $$$$=\overset{{n}} {\sum}\frac{{n}+\mathrm{2}+{n}−\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}=\overset{{n}} {\sum}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}+\overset{{n}} {\sum}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)}−\overset{{n}} {\sum}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)} \\ $$$$=\overset{{n}} {\sum}\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}+\overset{{n}} {\sum}\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\overset{{n}} {\sum}\frac{{n}+\mathrm{2}−{n}}{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right)+\left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\overset{{n}} {\sum}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}}\overset{{n}} {\sum}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right)+\left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\overset{{n}} {\sum}\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\overset{{n}} {\sum}\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{2}} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right)+\left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$
Answered by mathmax by abdo last updated on 06/Aug/20
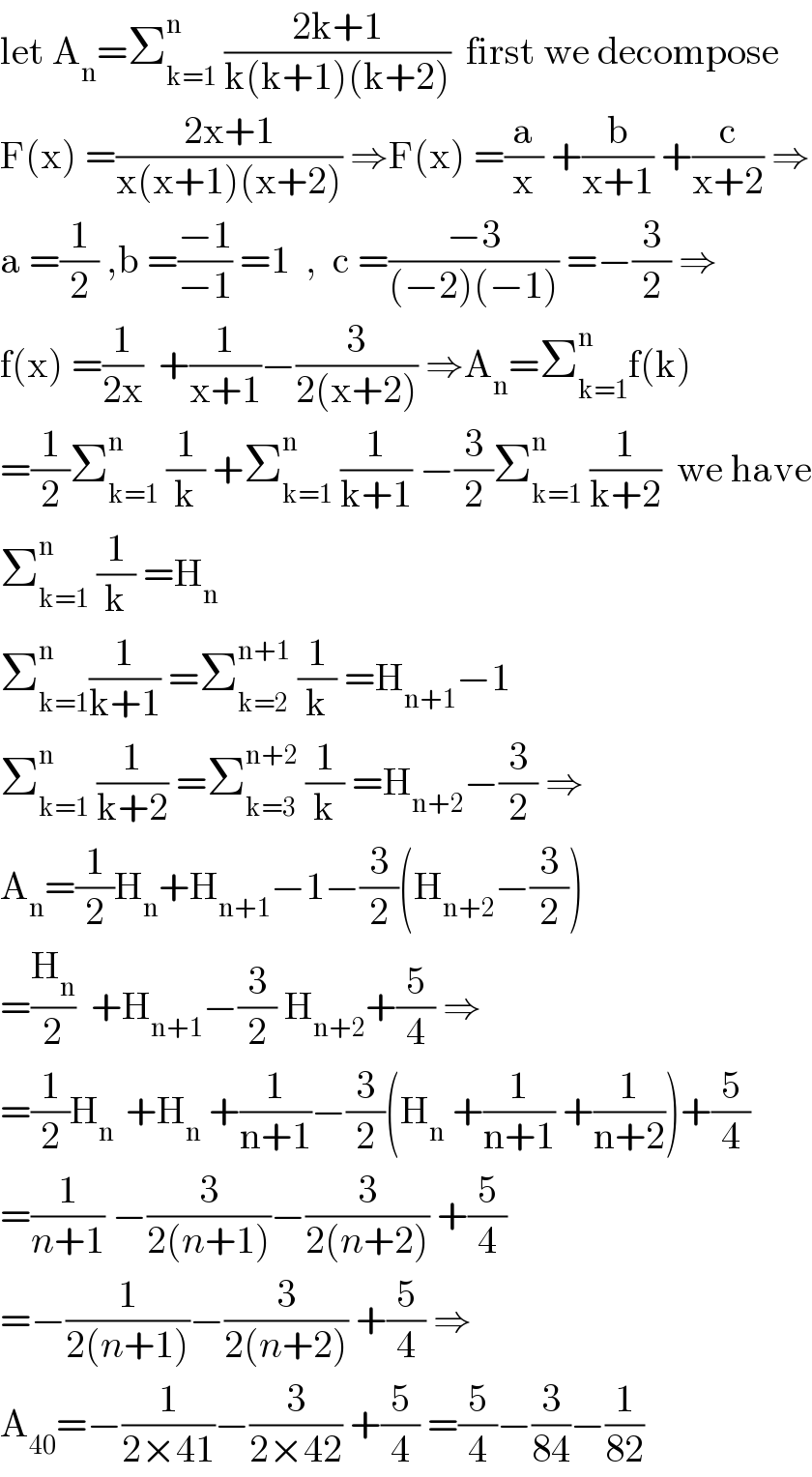
let A_n =Σ_(k=1) ^n ((2k+1)/(k(k+1)(k+2))) first we decompose F(x) =((2x+1)/(x(x+1)(x+2))) ⇒F(x) =(a/x) +(b/(x+1)) +(c/(x+2)) ⇒ a =(1/2) ,b =((−1)/(−1)) =1 , c =((−3)/((−2)(−1))) =−(3/2) ⇒ f(x) =(1/(2x)) +(1/(x+1))−(3/(2(x+2))) ⇒A_n =Σ_(k=1) ^n f(k) =(1/2)Σ_(k=1) ^n (1/k) +Σ_(k=1) ^n (1/(k+1)) −(3/2)Σ_(k=1) ^n (1/(k+2)) we have Σ_(k=1) ^n (1/k) =H_n Σ_(k=1) ^n (1/(k+1)) =Σ_(k=2) ^(n+1) (1/k) =H_(n+1) −1 Σ_(k=1) ^n (1/(k+2)) =Σ_(k=3) ^(n+2) (1/k) =H_(n+2) −(3/2) ⇒ A_n =(1/2)H_n +H_(n+1) −1−(3/2)(H_(n+2) −(3/2)) =(H_n /2) +H_(n+1) −(3/2) H_(n+2) +(5/4) ⇒ =(1/2)H_(n ) +H_n +(1/(n+1))−(3/2)(H_n +(1/(n+1)) +(1/(n+2)))+(5/4) =(1/(n+1)) −(3/(2(n+1)))−(3/(2(n+2))) +(5/4) =−(1/(2(n+1)))−(3/(2(n+2))) +(5/4) ⇒ A_(40) =−(1/(2×41))−(3/(2×42)) +(5/4) =(5/4)−(3/(84))−(1/(82))
$$\mathrm{let}\:\mathrm{A}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{2k}+\mathrm{1}}{\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right)}\:\:\mathrm{first}\:\mathrm{we}\:\mathrm{decompose} \\ $$$$\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)}\:\Rightarrow\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{a}}{\mathrm{x}}\:+\frac{\mathrm{b}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{c}}{\mathrm{x}+\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{a}\:=\frac{\mathrm{1}}{\mathrm{2}}\:,\mathrm{b}\:=\frac{−\mathrm{1}}{−\mathrm{1}}\:=\mathrm{1}\:\:,\:\:\mathrm{c}\:=\frac{−\mathrm{3}}{\left(−\mathrm{2}\right)\left(−\mathrm{1}\right)}\:=−\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{2x}}\:\:+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}−\frac{\mathrm{3}}{\mathrm{2}\left(\mathrm{x}+\mathrm{2}\right)}\:\Rightarrow\mathrm{A}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \mathrm{f}\left(\mathrm{k}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}}\:+\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}\:−\frac{\mathrm{3}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{2}}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}}\:=\mathrm{H}_{\mathrm{n}} \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}\:=\sum_{\mathrm{k}=\mathrm{2}} ^{\mathrm{n}+\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{k}}\:=\mathrm{H}_{\mathrm{n}+\mathrm{1}} −\mathrm{1} \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{2}}\:=\sum_{\mathrm{k}=\mathrm{3}} ^{\mathrm{n}+\mathrm{2}} \:\frac{\mathrm{1}}{\mathrm{k}}\:=\mathrm{H}_{\mathrm{n}+\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{H}_{\mathrm{n}} +\mathrm{H}_{\mathrm{n}+\mathrm{1}} −\mathrm{1}−\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{H}_{\mathrm{n}+\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{H}_{\mathrm{n}} }{\mathrm{2}}\:\:+\mathrm{H}_{\mathrm{n}+\mathrm{1}} −\frac{\mathrm{3}}{\mathrm{2}}\:\mathrm{H}_{\mathrm{n}+\mathrm{2}} +\frac{\mathrm{5}}{\mathrm{4}}\:\Rightarrow \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{H}_{\mathrm{n}\:} \:+\mathrm{H}_{\mathrm{n}} \:+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{H}_{\mathrm{n}} \:+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}\right)+\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}}\:−\frac{\mathrm{3}}{\mathrm{2}\left({n}+\mathrm{1}\right)}−\frac{\mathrm{3}}{\mathrm{2}\left({n}+\mathrm{2}\right)}\:+\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}−\frac{\mathrm{3}}{\mathrm{2}\left({n}+\mathrm{2}\right)}\:+\frac{\mathrm{5}}{\mathrm{4}}\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{40}} =−\frac{\mathrm{1}}{\mathrm{2}×\mathrm{41}}−\frac{\mathrm{3}}{\mathrm{2}×\mathrm{42}}\:+\frac{\mathrm{5}}{\mathrm{4}}\:=\frac{\mathrm{5}}{\mathrm{4}}−\frac{\mathrm{3}}{\mathrm{84}}−\frac{\mathrm{1}}{\mathrm{82}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *