Menu Close

Question-106745

Tinku Tara 0 Comments
Pin




Question Number 106745 by qwertyu last updated on 06/Aug/20
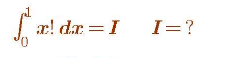
Commented by Her_Majesty last updated on 06/Aug/20
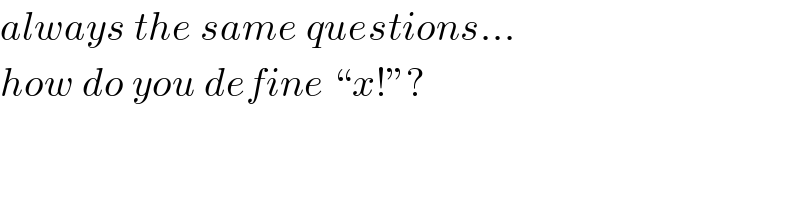
always the same questions... how do you define “x!”?
$${always}\:{the}\:{same}\:{questions}… \\ $$$${how}\:{do}\:{you}\:{define}\:“{x}!''? \\ $$
Commented by qwertyu last updated on 06/Aug/20
∫_0 ^( 1) x! = ?
$$\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \:\boldsymbol{{x}}!\:=\:? \\ $$
Commented by Her_Majesty last updated on 06/Aug/20
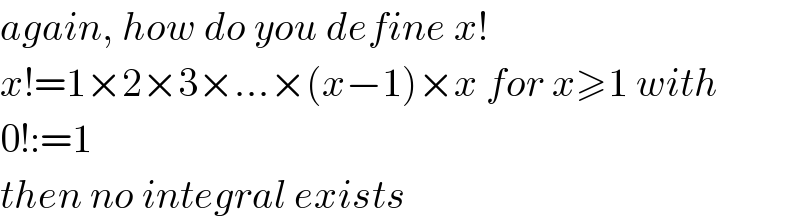
again, how do you define x! x!=1×2×3×...×(x−1)×x for x≥1 with 0!:=1 then no integral exists
$${again},\:{how}\:{do}\:{you}\:{define}\:{x}! \\ $$$${x}!=\mathrm{1}×\mathrm{2}×\mathrm{3}×…×\left({x}−\mathrm{1}\right)×{x}\:{for}\:{x}\geqslant\mathrm{1}\:{with} \\ $$$$\mathrm{0}!:=\mathrm{1} \\ $$$${then}\:{no}\:{integral}\:{exists} \\ $$
Commented by floor(10²Eta[1]) last updated on 06/Aug/20
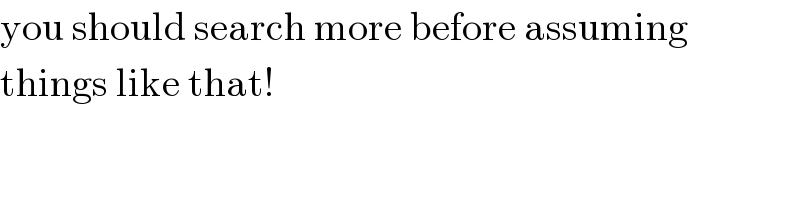
you should search more before assuming things like that!
$$\mathrm{you}\:\mathrm{should}\:\mathrm{search}\:\mathrm{more}\:\mathrm{before}\:\mathrm{assuming} \\ $$$$\mathrm{things}\:\mathrm{like}\:\mathrm{that}! \\ $$
Commented by floor(10²Eta[1]) last updated on 06/Aug/20
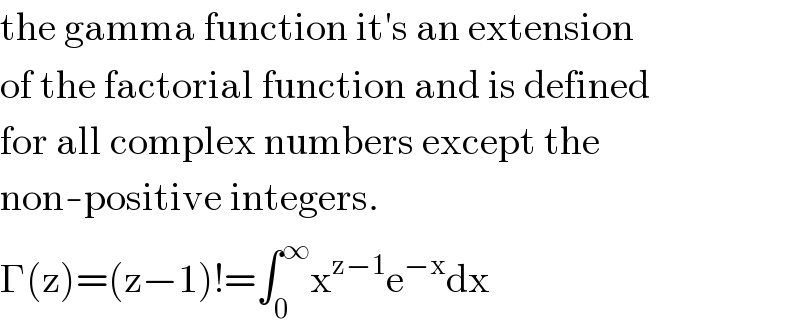
the gamma function it′s an extension of the factorial function and is defined for all complex numbers except the non-positive integers. Γ(z)=(z−1)!=∫_0 ^∞ x^(z−1) e^(−x) dx
$$\mathrm{the}\:\mathrm{gamma}\:\mathrm{function}\:\mathrm{it}'\mathrm{s}\:\mathrm{an}\:\mathrm{extension} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{factorial}\:\mathrm{function}\:\mathrm{and}\:\mathrm{is}\:\mathrm{defined} \\ $$$$\mathrm{for}\:\mathrm{all}\:\mathrm{complex}\:\mathrm{numbers}\:\mathrm{except}\:\mathrm{the}\: \\ $$$$\mathrm{non}-\mathrm{positive}\:\mathrm{integers}. \\ $$$$\Gamma\left(\mathrm{z}\right)=\left(\mathrm{z}−\mathrm{1}\right)!=\int_{\mathrm{0}} ^{\infty} \mathrm{x}^{\mathrm{z}−\mathrm{1}} \mathrm{e}^{−\mathrm{x}} \mathrm{dx} \\ $$
Commented by Her_Majesty last updated on 06/Aug/20
I know these things, don′t have to search But I often wonder if the posters of these questions know what they are posting as you wrote Γ(x+1) is the extension of x! but nonetheless ∫x!dx doesn′t exist; only the extension ∫Γ(x+1)dx exists you guys don′t do proper maths sometimes it seems
$${I}\:{know}\:{these}\:{things},\:{don}'{t}\:{have}\:{to}\:{search} \\ $$$${But}\:{I}\:{often}\:{wonder}\:{if}\:{the}\:{posters}\:{of}\:{these} \\ $$$${questions}\:{know}\:{what}\:{they}\:{are}\:{posting} \\ $$$$ \\ $$$${as}\:{you}\:{wrote}\:\Gamma\left({x}+\mathrm{1}\right)\:{is}\:{the}\:{extension}\:{of}\:{x}! \\ $$$${but}\:{nonetheless}\:\int{x}!{dx}\:{doesn}'{t}\:{exist};\:{only} \\ $$$${the}\:{extension}\:\int\Gamma\left({x}+\mathrm{1}\right){dx}\:{exists} \\ $$$$ \\ $$$${you}\:{guys}\:{don}'{t}\:{do}\:{proper}\:{maths}\:{sometimes} \\ $$$${it}\:{seems} \\ $$
Commented by Sarah85 last updated on 07/Aug/20
it′s another pandemic it seems...
$$\mathrm{it}'\mathrm{s}\:\mathrm{another}\:\mathrm{pandemic}\:\mathrm{it}\:\mathrm{seems}… \\ $$
Commented by 1549442205PVT last updated on 07/Aug/20
Since the function x! isn′t a continue function ,it is interrupt everywhere ,so don′t exist defined integral ∫_a ^b x!dx
$$\mathrm{Since}\:\mathrm{the}\:\mathrm{function}\:\mathrm{x}!\:\mathrm{isn}'\mathrm{t}\:\mathrm{a}\:\mathrm{continue} \\ $$$$\mathrm{function}\:,\mathrm{it}\:\mathrm{is}\:\mathrm{interrupt}\:\mathrm{everywhere} \\ $$$$,\mathrm{so}\:\mathrm{don}'\mathrm{t}\:\mathrm{exist}\:\mathrm{defined}\:\mathrm{integral}\:\int_{\mathrm{a}} ^{\mathrm{b}} \mathrm{x}!\mathrm{dx} \\ $$
Answered by mathmax by abdo last updated on 06/Aug/20
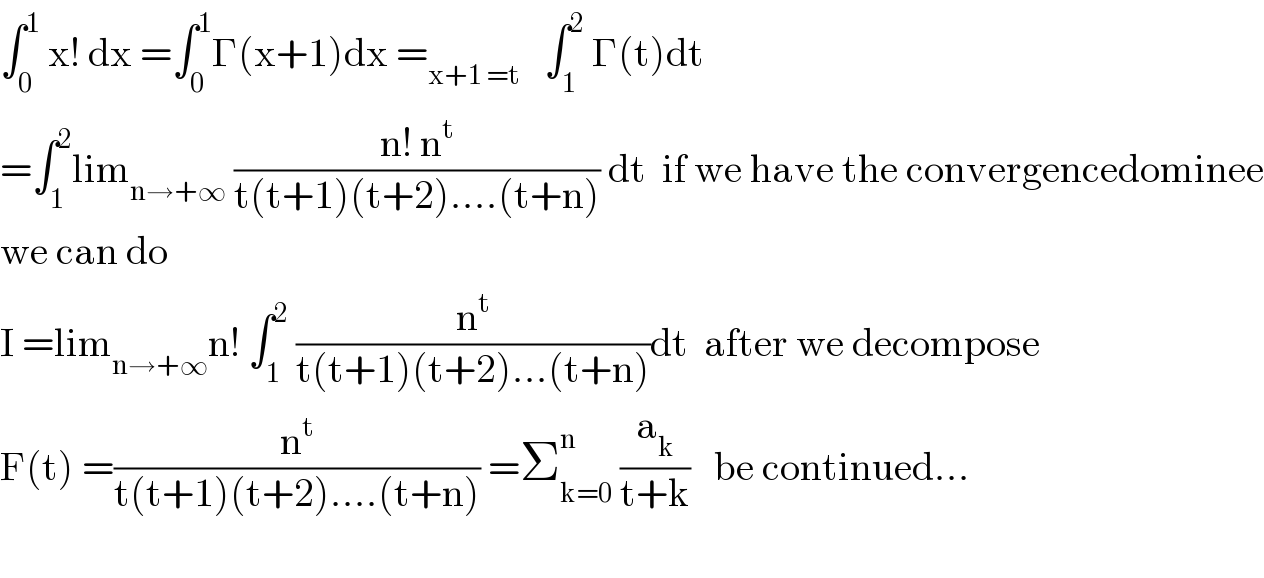
∫_0 ^1 x! dx =∫_0 ^1 Γ(x+1)dx =_(x+1 =t) ∫_1 ^2 Γ(t)dt =∫_1 ^2 lim_(n→+∞) ((n! n^t )/(t(t+1)(t+2)....(t+n))) dt if we have the convergencedominee we can do I =lim_(n→+∞) n! ∫_1 ^2 (n^t /(t(t+1)(t+2)...(t+n)))dt after we decompose F(t) =(n^t /(t(t+1)(t+2)....(t+n))) =Σ_(k=0) ^n (a_k /(t+k)) be continued...
$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}!\:\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \Gamma\left(\mathrm{x}+\mathrm{1}\right)\mathrm{dx}\:=_{\mathrm{x}+\mathrm{1}\:=\mathrm{t}} \:\:\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\Gamma\left(\mathrm{t}\right)\mathrm{dt}\: \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\frac{\mathrm{n}!\:\mathrm{n}^{\mathrm{t}} }{\mathrm{t}\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}+\mathrm{2}\right)….\left(\mathrm{t}+\mathrm{n}\right)}\:\mathrm{dt}\:\:\mathrm{if}\:\mathrm{we}\:\mathrm{have}\:\mathrm{the}\:\mathrm{convergencedominee} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{do} \\ $$$$\mathrm{I}\:=\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{n}!\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{\mathrm{n}^{\mathrm{t}} }{\mathrm{t}\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}+\mathrm{2}\right)…\left(\mathrm{t}+\mathrm{n}\right)}\mathrm{dt}\:\:\mathrm{after}\:\mathrm{we}\:\mathrm{decompose} \\ $$$$\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{n}^{\mathrm{t}} }{\mathrm{t}\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}+\mathrm{2}\right)….\left(\mathrm{t}+\mathrm{n}\right)}\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{a}_{\mathrm{k}} }{\mathrm{t}+\mathrm{k}}\:\:\:\mathrm{be}\:\mathrm{continued}… \\ $$$$ \\ $$
Answered by Sarah85 last updated on 07/Aug/20
∫_0 ^1 Γ(x+1)dx≈.922 745 950 259
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\Gamma\left({x}+\mathrm{1}\right){dx}\approx.\mathrm{922}\:\mathrm{745}\:\mathrm{950}\:\mathrm{259} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *