Question Number 106956 by bemath last updated on 08/Aug/20
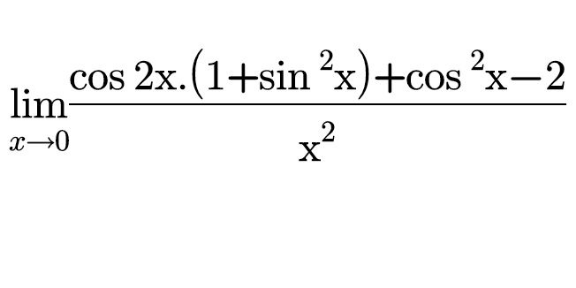
Answered by 1549442205PVT last updated on 08/Aug/20
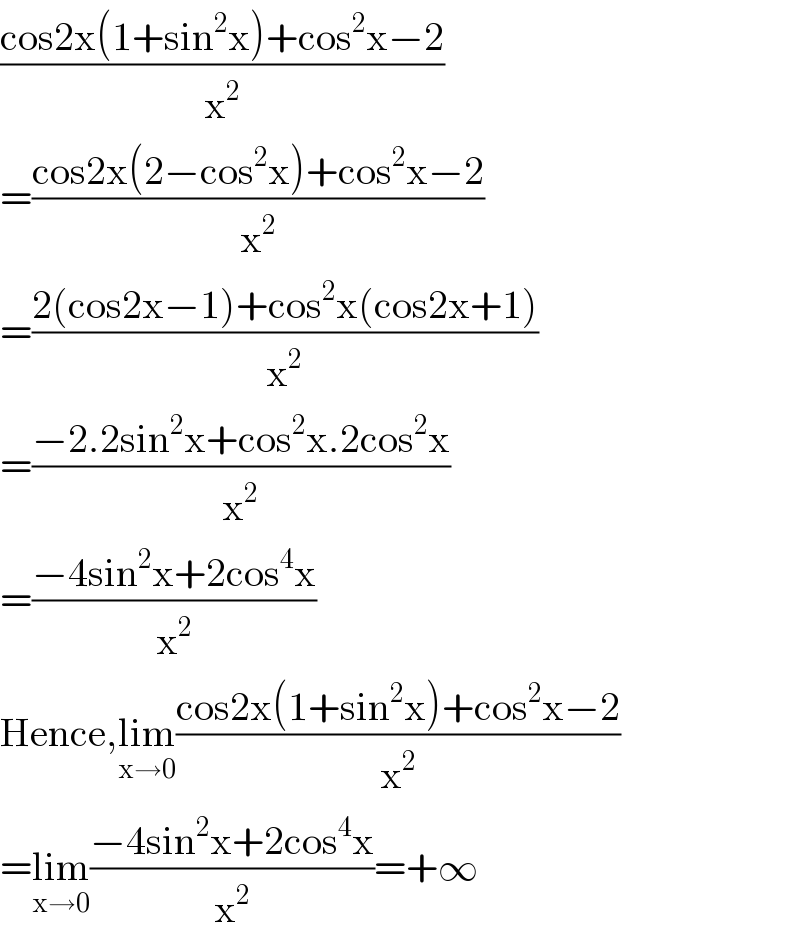
$$\frac{\mathrm{cos2x}\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)+\mathrm{cos}^{\mathrm{2}} \mathrm{x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{cos2x}\left(\mathrm{2}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)+\mathrm{cos}^{\mathrm{2}} \mathrm{x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}\left(\mathrm{cos2x}−\mathrm{1}\right)+\mathrm{cos}^{\mathrm{2}} \mathrm{x}\left(\mathrm{cos2x}+\mathrm{1}\right)}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{2}.\mathrm{2sin}^{\mathrm{2}} \mathrm{x}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}.\mathrm{2cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{4sin}^{\mathrm{2}} \mathrm{x}+\mathrm{2cos}^{\mathrm{4}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{Hence},\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos2x}\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)+\mathrm{cos}^{\mathrm{2}} \mathrm{x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{4sin}^{\mathrm{2}} \mathrm{x}+\mathrm{2cos}^{\mathrm{4}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} }=+\infty \\ $$
Commented by bemath last updated on 10/Aug/20

$${wrong} \\ $$
Answered by bemath last updated on 08/Aug/20
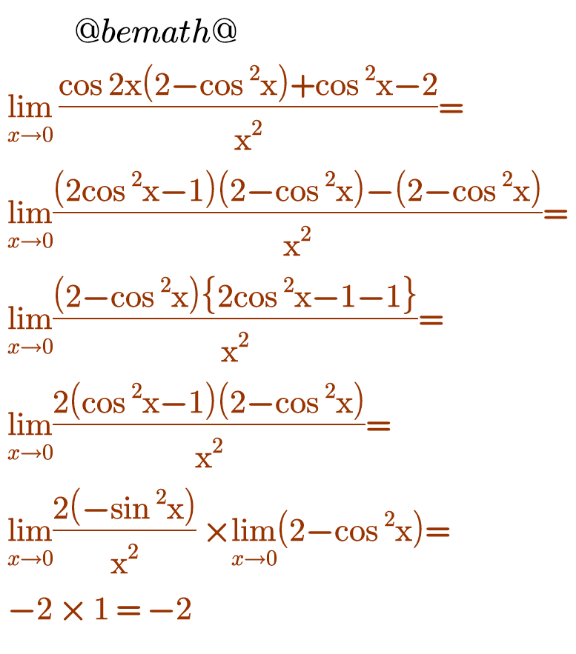
Answered by Dwaipayan Shikari last updated on 08/Aug/20
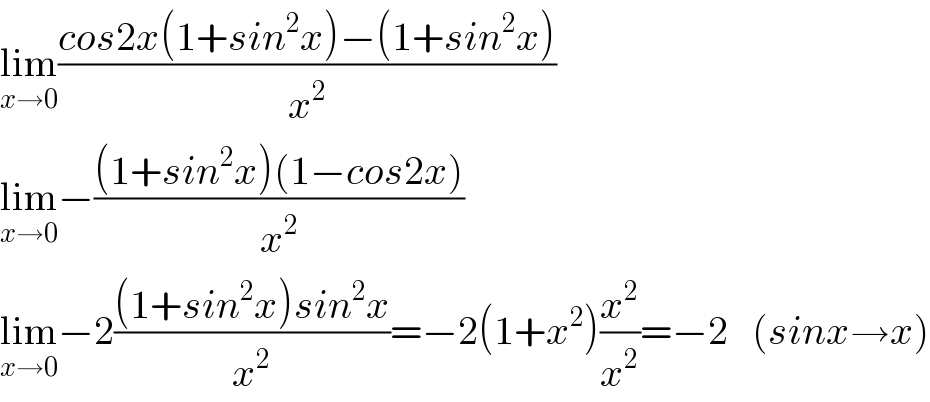
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{cos}\mathrm{2}{x}\left(\mathrm{1}+{sin}^{\mathrm{2}} {x}\right)−\left(\mathrm{1}+{sin}^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}−\frac{\left(\mathrm{1}+{sin}^{\mathrm{2}} {x}\right)\left(\mathrm{1}−{cos}\mathrm{2}{x}\right)}{{x}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}−\mathrm{2}\frac{\left(\mathrm{1}+{sin}^{\mathrm{2}} {x}\right){sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }=−\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }=−\mathrm{2}\:\:\:\left({sinx}\rightarrow{x}\right) \\ $$
