Menu Close

Question-106977

Tinku Tara 0 Comments
Pin




Question Number 106977 by mr W last updated on 08/Aug/20
Answered by mr W last updated on 08/Aug/20
A(a,0) and B(b,0) P lies on y=x^2 find the minimum of perimeter of ΔPAB.
$${A}\left({a},\mathrm{0}\right)\:{and}\:{B}\left({b},\mathrm{0}\right) \\ $$$${P}\:{lies}\:{on}\:{y}={x}^{\mathrm{2}} \\ $$$${find}\:{the}\:{minimum}\:{of}\:{perimeter}\:{of} \\ $$$$\Delta{PAB}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 08/Aug/20
(b−a)+ (√(a^2 +b^2 ))
$$\left(\mathrm{b}−\mathrm{a}\right)+\:\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} } \\ $$
Answered by mr W last updated on 08/Aug/20
METHOD I say P(p,p^2 ) tangent at P is y=p^2 +2p(x−p) ⇒2px−y−p^2 =0 image of B in tangent is C(x_C ,y_C ) x_C =b−((4p(2pb−p^2 ))/(4p^2 +1)) y_C =((2(2pb−p^2 ))/(4p^2 +1)) A,P,C are collinear, ((y_C −p^2 )/p^2 )=((x_C −p)/(p−a)) ((2(2pb−p^2 ))/(4p^2 +1))−p^2 =(p^2 /(p−a))[b−((4p(2pb−p^2 ))/(4p^2 +1))−p] ⇒p^4 −(a+b)p^3 +(1/2)p^2 −(3/4)(a+b)p+ab=0 ⇒p=....
$$\boldsymbol{{METHOD}}\:\boldsymbol{{I}} \\ $$$${say}\:{P}\left({p},{p}^{\mathrm{2}} \right) \\ $$$${tangent}\:{at}\:{P}\:{is} \\ $$$${y}={p}^{\mathrm{2}} +\mathrm{2}{p}\left({x}−{p}\right) \\ $$$$\Rightarrow\mathrm{2}{px}−{y}−{p}^{\mathrm{2}} =\mathrm{0} \\ $$$${image}\:{of}\:{B}\:{in}\:{tangent}\:{is}\:{C}\left({x}_{{C}} ,{y}_{{C}} \right) \\ $$$${x}_{{C}} ={b}−\frac{\mathrm{4}{p}\left(\mathrm{2}{pb}−{p}^{\mathrm{2}} \right)}{\mathrm{4}{p}^{\mathrm{2}} +\mathrm{1}} \\ $$$${y}_{{C}} =\frac{\mathrm{2}\left(\mathrm{2}{pb}−{p}^{\mathrm{2}} \right)}{\mathrm{4}{p}^{\mathrm{2}} +\mathrm{1}} \\ $$$${A},{P},{C}\:{are}\:{collinear}, \\ $$$$\frac{{y}_{{C}} −{p}^{\mathrm{2}} }{{p}^{\mathrm{2}} }=\frac{{x}_{{C}} −{p}}{{p}−{a}} \\ $$$$\frac{\mathrm{2}\left(\mathrm{2}{pb}−{p}^{\mathrm{2}} \right)}{\mathrm{4}{p}^{\mathrm{2}} +\mathrm{1}}−{p}^{\mathrm{2}} =\frac{{p}^{\mathrm{2}} }{{p}−{a}}\left[{b}−\frac{\mathrm{4}{p}\left(\mathrm{2}{pb}−{p}^{\mathrm{2}} \right)}{\mathrm{4}{p}^{\mathrm{2}} +\mathrm{1}}−{p}\right] \\ $$$$\Rightarrow{p}^{\mathrm{4}} −\left({a}+{b}\right){p}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{2}}{p}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}\left({a}+{b}\right){p}+{ab}=\mathrm{0} \\ $$$$\Rightarrow{p}=…. \\ $$
Commented by PRITHWISH SEN 2 last updated on 08/Aug/20
Sir, whether this image concept applicable in this case ? Because the point A and B are fixed. What do you think sir ?
$$\mathrm{Sir},\:\mathrm{whether}\:\mathrm{this}\:\mathrm{image}\:\mathrm{concept}\:\mathrm{applicable}\:\mathrm{in}\:\mathrm{this} \\ $$$$\mathrm{case}\:?\:\mathrm{Because}\:\mathrm{the}\:\mathrm{point}\:\mathrm{A}\:\mathrm{and}\:\mathrm{B}\:\mathrm{are}\:\mathrm{fixed}.\:\mathrm{What} \\ $$$$\mathrm{do}\:\mathrm{you}\:\mathrm{think}\:\mathrm{sir}\:? \\ $$
Commented by mr W last updated on 08/Aug/20
Commented by mr W last updated on 08/Aug/20
the shortest path A−P−B is that one which a light ray from A to B follows. that means the tangent at point P should act like a mirror.
$${the}\:{shortest}\:{path}\:{A}−{P}−{B}\:{is}\:{that}\:{one} \\ $$$${which}\:{a}\:{light}\:{ray}\:{from}\:{A}\:{to}\:{B}\:{follows}. \\ $$$${that}\:{means}\:{the}\:{tangent}\:{at}\:{point}\:{P} \\ $$$${should}\:{act}\:{like}\:{a}\:{mirror}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 08/Aug/20
yes sir but the oriantation of the tangent is changing at every point . A−P−B^′ can′t be the straight line always. Can PB′ (B′ the image of B) be colinear with AB′ ?
$$\mathrm{yes}\:\mathrm{sir}\:\mathrm{but}\:\mathrm{the}\:\mathrm{oriantation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{tangent}\:\mathrm{is}\: \\ $$$$\mathrm{changing}\:\mathrm{at}\:\mathrm{every}\:\mathrm{point}\:.\:\mathrm{A}−\mathrm{P}−\mathrm{B}^{'} \:\mathrm{can}'\mathrm{t}\:\mathrm{be}\:\mathrm{the} \\ $$$$\mathrm{straight}\:\mathrm{line}\:\mathrm{always}.\:\mathrm{Can}\:\mathrm{PB}'\:\left(\mathrm{B}'\:\mathrm{the}\:\mathrm{image}\:\mathrm{of}\right. \\ $$$$\left.\mathrm{B}\right)\:\mathrm{be}\:\mathrm{colinear}\:\mathrm{with}\:\mathrm{AB}'\:? \\ $$
Commented by mr W last updated on 08/Aug/20
only that point P is the right one, when the image of B, i.e. point C is collinear with A and P. there is only one such a point P.
$${only}\:{that}\:{point}\:{P}\:{is}\:{the}\:{right}\:{one}, \\ $$$${when}\:{the}\:{image}\:{of}\:{B},\:{i}.{e}.\:{point}\:{C}\:{is} \\ $$$${collinear}\:{with}\:{A}\:{and}\:{P}.\:{there}\:{is}\:{only} \\ $$$${one}\:{such}\:{a}\:{point}\:{P}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 08/Aug/20
OK sir now it is clear.
$$\mathrm{OK}\:\mathrm{sir}\:\mathrm{now}\:\mathrm{it}\:\mathrm{is}\:\mathrm{clear}. \\ $$
Commented by mr W last updated on 08/Aug/20
image the parabolla is curved mirror and you stand at point A. now you direct at a point at the mirror with a laser pointer. the laser beam will be reflected by the mirror. only when the reflected laser beam meets the point B, you have got the shortest path.
$${image}\:{the}\:{parabolla}\:{is}\:{curved}\:{mirror} \\ $$$${and}\:{you}\:{stand}\:{at}\:{point}\:{A}.\:{now}\:{you}\: \\ $$$${direct}\:{at}\:{a}\:{point}\:{at}\:{the}\:{mirror}\:{with} \\ $$$${a}\:{laser}\:{pointer}.\:{the}\:{laser}\:{beam}\:{will}\:{be} \\ $$$${reflected}\:{by}\:{the}\:{mirror}.\:{only}\:{when} \\ $$$${the}\:{reflected}\:{laser}\:{beam}\:{meets}\:{the} \\ $$$${point}\:{B},\:{you}\:{have}\:{got}\:{the}\:{shortest} \\ $$$${path}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 08/Aug/20
thank you sir
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 08/Aug/20
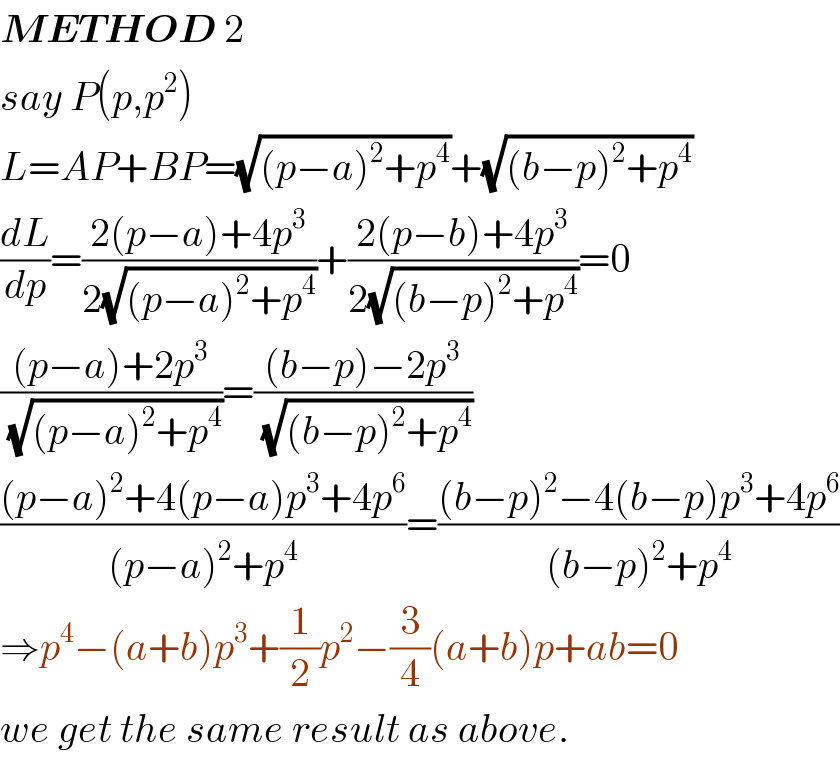
METHOD 2 say P(p,p^2 ) L=AP+BP=(√((p−a)^2 +p^4 ))+(√((b−p)^2 +p^4 )) (dL/dp)=((2(p−a)+4p^3 )/(2(√((p−a)^2 +p^4 ))))+((2(p−b)+4p^3 )/(2(√((b−p)^2 +p^4 ))))=0 (((p−a)+2p^3 )/( (√((p−a)^2 +p^4 ))))=(((b−p)−2p^3 )/( (√((b−p)^2 +p^4 )))) (((p−a)^2 +4(p−a)p^3 +4p^6 )/((p−a)^2 +p^4 ))=(((b−p)^2 −4(b−p)p^3 +4p^6 )/((b−p)^2 +p^4 )) ⇒p^4 −(a+b)p^3 +(1/2)p^2 −(3/4)(a+b)p+ab=0 we get the same result as above.
$$\boldsymbol{{METHOD}}\:\mathrm{2} \\ $$$${say}\:{P}\left({p},{p}^{\mathrm{2}} \right) \\ $$$${L}={AP}+{BP}=\sqrt{\left({p}−{a}\right)^{\mathrm{2}} +{p}^{\mathrm{4}} }+\sqrt{\left({b}−{p}\right)^{\mathrm{2}} +{p}^{\mathrm{4}} } \\ $$$$\frac{{dL}}{{dp}}=\frac{\mathrm{2}\left({p}−{a}\right)+\mathrm{4}{p}^{\mathrm{3}} }{\mathrm{2}\sqrt{\left({p}−{a}\right)^{\mathrm{2}} +{p}^{\mathrm{4}} }}+\frac{\mathrm{2}\left({p}−{b}\right)+\mathrm{4}{p}^{\mathrm{3}} }{\mathrm{2}\sqrt{\left({b}−{p}\right)^{\mathrm{2}} +{p}^{\mathrm{4}} }}=\mathrm{0} \\ $$$$\frac{\left({p}−{a}\right)+\mathrm{2}{p}^{\mathrm{3}} }{\:\sqrt{\left({p}−{a}\right)^{\mathrm{2}} +{p}^{\mathrm{4}} }}=\frac{\left({b}−{p}\right)−\mathrm{2}{p}^{\mathrm{3}} }{\:\sqrt{\left({b}−{p}\right)^{\mathrm{2}} +{p}^{\mathrm{4}} }} \\ $$$$\frac{\left({p}−{a}\right)^{\mathrm{2}} +\mathrm{4}\left({p}−{a}\right){p}^{\mathrm{3}} +\mathrm{4}{p}^{\mathrm{6}} }{\left({p}−{a}\right)^{\mathrm{2}} +{p}^{\mathrm{4}} }=\frac{\left({b}−{p}\right)^{\mathrm{2}} −\mathrm{4}\left({b}−{p}\right){p}^{\mathrm{3}} +\mathrm{4}{p}^{\mathrm{6}} }{\left({b}−{p}\right)^{\mathrm{2}} +{p}^{\mathrm{4}} } \\ $$$$\Rightarrow{p}^{\mathrm{4}} −\left({a}+{b}\right){p}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{2}}{p}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}\left({a}+{b}\right){p}+{ab}=\mathrm{0} \\ $$$${we}\:{get}\:{the}\:{same}\:{result}\:{as}\:{above}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *