Question Number 106983 by Khalmohmmad last updated on 08/Aug/20
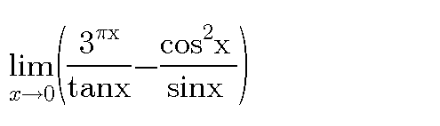
Answered by bemath last updated on 08/Aug/20
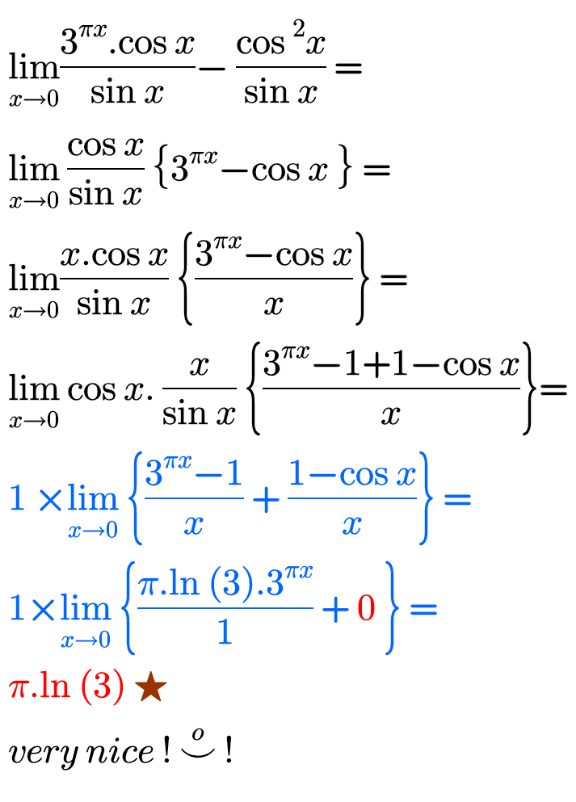
Answered by Dwaipayan Shikari last updated on 08/Aug/20
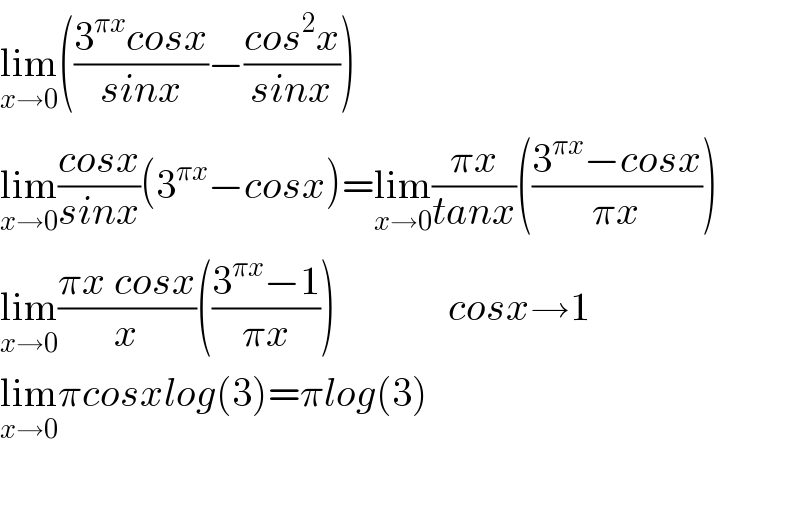
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{3}^{\pi{x}} {cosx}}{{sinx}}−\frac{{cos}^{\mathrm{2}} {x}}{{sinx}}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{cosx}}{{sinx}}\left(\mathrm{3}^{\pi{x}} −{cosx}\right)=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\pi{x}}{{tanx}}\left(\frac{\mathrm{3}^{\pi{x}} −{cosx}}{\pi{x}}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\pi{x}\:{cosx}}{{x}}\left(\frac{\mathrm{3}^{\pi{x}} −\mathrm{1}}{\pi{x}}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:{cosx}\rightarrow\mathrm{1} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\pi{cosxlog}\left(\mathrm{3}\right)=\pi{log}\left(\mathrm{3}\right) \\ $$$$ \\ $$
