Question Number 107034 by mathdave last updated on 08/Aug/20

Commented by kaivan.ahmadi last updated on 08/Aug/20

$$=\frac{\sqrt{\mathrm{2}}\mid{sin}\mathrm{6}\pi\mid}{\:\sqrt{\mathrm{1}−{cos}\pi}}=\frac{\mathrm{0}}{\:\sqrt{\mathrm{1}−\left(−\mathrm{1}\right)}}=\frac{\mathrm{0}}{\:\sqrt{\mathrm{2}}}=\mathrm{0} \\ $$
Commented by kaivan.ahmadi last updated on 08/Aug/20

$${sin}\mathrm{6}\pi=\mathrm{0}\:{and}\:{cos}\pi=−\mathrm{1} \\ $$$$ \\ $$
Commented by kaivan.ahmadi last updated on 08/Aug/20
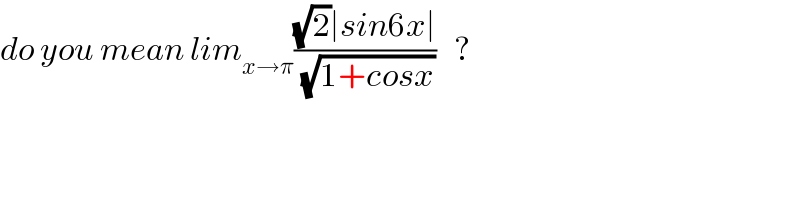
$${do}\:{you}\:{mean}\:{lim}_{{x}\rightarrow\pi} \frac{\sqrt{\mathrm{2}}\mid{sin}\mathrm{6}{x}\mid}{\:\sqrt{\mathrm{1}+{cosx}}}\:\:\:? \\ $$
Commented by mathdave last updated on 08/Aug/20

$${yah} \\ $$
Commented by 1549442205PVT last updated on 08/Aug/20

$$\mathrm{If}\:\mathrm{the}\:\mathrm{question}\:\mathrm{was}\:\mathrm{corrected}\:\mathrm{such}\:\mathrm{as} \\ $$$$\mathrm{then}\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{follows}\:\mathrm{as}: \\ $$$$\mathrm{L}{im}_{{x}\rightarrow\pi} \frac{\sqrt{\mathrm{2}}\mid{sin}\mathrm{6}{x}\mid}{\:\sqrt{\mathrm{1}+{cosx}}}\:\:\:=\underset{\mathrm{x}\rightarrow\pi} {\mathrm{lim}}\frac{\sqrt{\mathrm{2}}\:\mid\mathrm{sin6x}\mid}{\:\sqrt{\mathrm{2cos}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}}} \\ $$$$=\underset{\mathrm{x}\rightarrow\pi} {\mathrm{lim}}\frac{\sqrt{\mathrm{2}}\:\mid\mathrm{sin6x}\mid}{\:\sqrt{\mathrm{2}}\:\mid\mathrm{cos}\frac{\mathrm{x}}{\mathrm{2}}\mid}=\underset{\mathrm{x}\rightarrow\pi} {\mathrm{lim}}\mid\frac{\mathrm{2sin3xcos3x}}{\mathrm{cos}\frac{\mathrm{x}}{\mathrm{2}}}\mid \\ $$$$=\underset{\mathrm{x}\rightarrow\pi} {\mathrm{lim}}\mid\frac{\mathrm{2}\left(\mathrm{3sinx}−\mathrm{4sin}^{\mathrm{3}} \mathrm{x}\right)\mathrm{cos3x}}{\mathrm{cos}\frac{\mathrm{x}}{\mathrm{2}}}\mid \\ $$$$=\mathrm{l}\underset{\mathrm{x}\rightarrow\pi} {\mathrm{im}}\mid\frac{\mathrm{sinx}}{\mathrm{cos}\frac{\mathrm{x}}{\mathrm{2}}}\mid.\mid\left(\mathrm{6}−\mathrm{8sin}^{\mathrm{2}} \mathrm{x}\right)\mathrm{cos3x}\mid \\ $$$$=\underset{\mathrm{x}\rightarrow\pi} {\mathrm{lim}}\mid\mathrm{2sin}\frac{\mathrm{x}}{\mathrm{2}}\mid.\mid\left(\mathrm{6}−\mathrm{8sin}^{\mathrm{2}} \mathrm{x}\right)\mathrm{cos3x}\mid \\ $$$$=\mathrm{2}.\mid\left(\mathrm{6}−\mathrm{8}\right).\left(−\mathrm{1}\right)\mid=\mathrm{4} \\ $$
Commented by john santu last updated on 09/Aug/20

$$\mid\left(\mathrm{6}−\mathrm{8sin}\:^{\mathrm{2}} \pi\right)\mathrm{cos}\:\mathrm{3}\pi\mid\:= \\ $$$$\mid\left(\mathrm{6}−\mathrm{0}\right).\left(−\mathrm{1}\right)\mid\:=\:\mathrm{6}?\:\: \\ $$
