Menu Close

Question-107088

Tinku Tara 0 Comments
Pin




Question Number 107088 by mathdave last updated on 08/Aug/20
Commented by mohammad17 last updated on 08/Aug/20
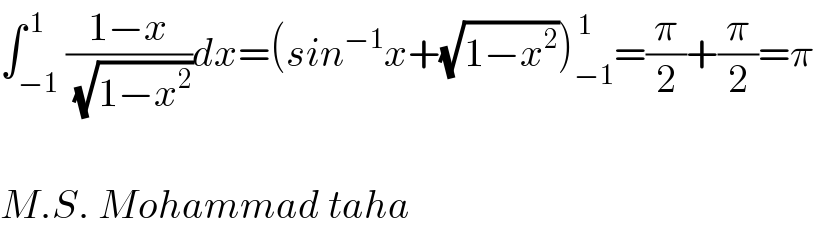
∫_(−1) ^( 1) ((1−x)/( (√(1−x^2 ))))dx=(sin^(−1) x+(√(1−x^2 )))_(−1) ^( 1) =(π/2)+(π/2)=π M.S. Mohammad taha
$$\int_{−\mathrm{1}} ^{\:\mathrm{1}} \frac{\mathrm{1}−{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}=\left({sin}^{−\mathrm{1}} {x}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)_{−\mathrm{1}} ^{\:\mathrm{1}} =\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}=\pi \\ $$$$ \\ $$$${M}.{S}.\:{Mohammad}\:{taha} \\ $$
Answered by abdomsup last updated on 08/Aug/20
another way we do the ch.(√((1−x)/(1+x)))=t ⇒((1−x)/(1+x)) =t^2 ⇒1−x=t^2 +t^2 x ⇒ (t^2 +1)x =1−t^2 ⇒x=((1−t^2 )/(1+t^2 )) ⇒ (dx/dt) =((−2t(1+t^2 )−2t(1−t^2 ))/((1+t^2 )^2 )) =((−2t −2t^3 −2t+2t^3 )/((1+t^2 )^2 )) =((−4t)/((1+t^2 )^2 )) ⇒ ∫_(−1) ^1 (√((1−x)/(1+x)))dx =−∫_0 ^(+∞) ((−4t^2 )/((1+t^2 )^2 ))dt =4 ∫_0 ^∞ ((1+t^2 −1)/((1+t^2 )^2 ))dt =4∫_0 ^∞ (dt/(1+t^2 ))−4∫_0 ^∞ (dt/((1+t^2 )^2 )) =2π−4∫_0 ^∞ (dt/((1+t^2 )^2 ))(ch. t=tanθ) =2π−4∫_0 ^(π/(2 )) ((1+tan^2 θ)/((1+tan^2 θ)^2 ))dθ =2π−4∫_0 ^(π/2) cos^2 θ dθ =2π−4∫_0 ^(π/2) ((1+cos(2θ))/2)dθ =π−2∫_0 ^(π/2) cos(2θ)dθ=π−0 =π
$${another}\:{way}\:{we}\:{do}\:{the}\:{ch}.\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}={t} \\ $$$$\Rightarrow\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\:={t}^{\mathrm{2}} \:\Rightarrow\mathrm{1}−{x}={t}^{\mathrm{2}} \:+{t}^{\mathrm{2}} {x}\:\Rightarrow \\ $$$$\left({t}^{\mathrm{2}} +\mathrm{1}\right){x}\:=\mathrm{1}−{t}^{\mathrm{2}} \:\Rightarrow{x}=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{{dx}}{{dt}}\:=\frac{−\mathrm{2}{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)−\mathrm{2}{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{2}{t}\:−\mathrm{2}{t}^{\mathrm{3}} −\mathrm{2}{t}+\mathrm{2}{t}^{\mathrm{3}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\frac{−\mathrm{4}{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}{dx}\:=−\int_{\mathrm{0}} ^{+\infty} \frac{−\mathrm{4}{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt} \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\infty} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }−\mathrm{4}\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\mathrm{2}\pi−\mathrm{4}\int_{\mathrm{0}} ^{\infty} \:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\left({ch}.\:{t}={tan}\theta\right) \\ $$$$=\mathrm{2}\pi−\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}\:}} \:\frac{\mathrm{1}+{tan}^{\mathrm{2}} \theta}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }{d}\theta \\ $$$$=\mathrm{2}\pi−\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}} \theta\:{d}\theta \\ $$$$=\mathrm{2}\pi−\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}{d}\theta \\ $$$$=\pi−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\left(\mathrm{2}\theta\right){d}\theta=\pi−\mathrm{0}\:=\pi \\ $$
Answered by abdomsup last updated on 08/Aug/20
I=∫_(−1) ^1 (√((1−x)/(1+x)))dx chsngrment x =cosθ give I =∫_π ^0 (√((1−cosθ)/(1+cosθ)))(−sinθ)dθ =∫_0 ^π ((sin((θ/2)))/(cos((θ/2))))(2sin((θ/2))cos((θ/2)))dθ =∫_0 ^π (1−cos(θ))dθ =π−[sinθ]_0 ^π =π ⇒I =π
$${I}=\int_{−\mathrm{1}} ^{\mathrm{1}} \:\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}{dx}\:\:{chsngrment} \\ $$$${x}\:={cos}\theta\:{give}\:{I}\:=\int_{\pi} ^{\mathrm{0}} \sqrt{\frac{\mathrm{1}−{cos}\theta}{\mathrm{1}+{cos}\theta}}\left(−{sin}\theta\right){d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\pi} \:\:\frac{{sin}\left(\frac{\theta}{\mathrm{2}}\right)}{{cos}\left(\frac{\theta}{\mathrm{2}}\right)}\left(\mathrm{2}{sin}\left(\frac{\theta}{\mathrm{2}}\right){cos}\left(\frac{\theta}{\mathrm{2}}\right)\right){d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\pi} \left(\mathrm{1}−{cos}\left(\theta\right)\right){d}\theta\:=\pi−\left[{sin}\theta\right]_{\mathrm{0}} ^{\pi} \\ $$$$=\pi\:\Rightarrow{I}\:=\pi \\ $$
Answered by Dwaipayan Shikari last updated on 08/Aug/20
∫_(−1) ^1 (√(((1−x)/(1+x)) )) dx ∫_(−1) ^1 ((1−x)/( (√(1−x^2 )))) dx=∫_(−1) ^1 (1/( (√(1−x^2 ))))+(1/2)∫_(−1) ^1 ((−2x)/( (√(1−x^2 )))) =[sin^(−1) x]_(−1) ^1 +[(1/2)(√(1−x^2 ))]_(−1) ^1 =(π/2)+(π/2)+0=π
$$\int_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}\:\:}\:\:\:\mathrm{dx} \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{1}−\mathrm{x}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx}=\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}+\frac{\mathrm{1}}{\mathrm{2}}\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{−\mathrm{2x}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }} \\ $$$$=\left[\mathrm{sin}^{−\mathrm{1}} \mathrm{x}\right]_{−\mathrm{1}} ^{\mathrm{1}} +\left[\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\right]_{−\mathrm{1}} ^{\mathrm{1}} \\ $$$$=\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}+\mathrm{0}=\pi \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *