Question-107107

Question Number 107107 by mohammad17 last updated on 08/Aug/20

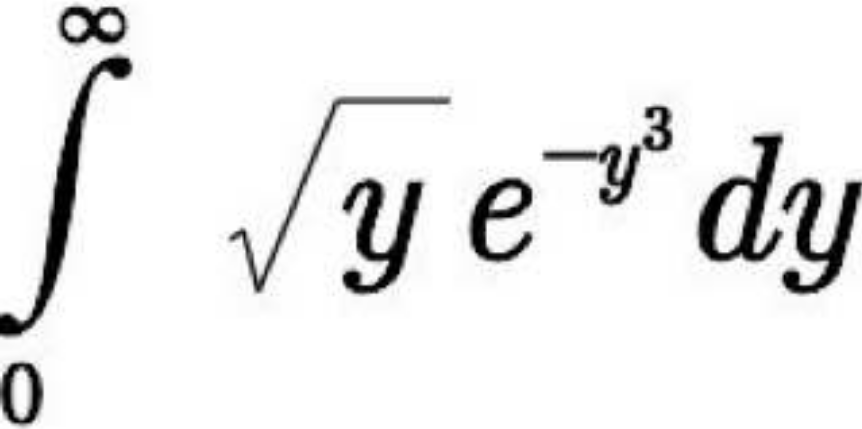
Commented by Dwaipayan Shikari last updated on 08/Aug/20

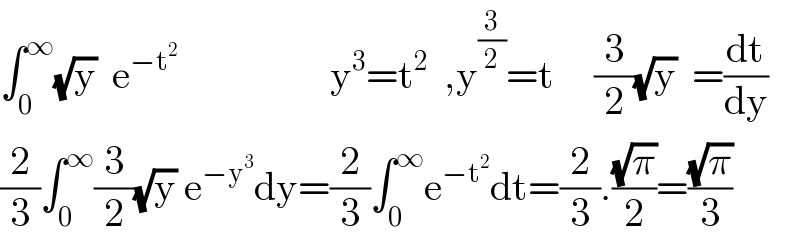
∫_0 ^∞ (√y) e^(−t^2 ) y^3 =t^(2 ) ,y^(3/2) =t (3/2)(√y) =(dt/dy) (2/3)∫_0 ^∞ (3/2)(√y) e^(−y^3 ) dy=(2/3)∫_0 ^∞ e^(−t^2 ) dt=(2/3).((√π)/2)=((√π)/3)

$$\int_{\mathrm{0}} ^{\infty} \sqrt{\mathrm{y}}\:\:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{y}^{\mathrm{3}} =\mathrm{t}^{\mathrm{2}\:\:} \:,\mathrm{y}^{\frac{\mathrm{3}}{\mathrm{2}}} =\mathrm{t}\:\:\:\:\:\frac{\mathrm{3}}{\mathrm{2}}\sqrt{\mathrm{y}}\:\:=\frac{\mathrm{dt}}{\mathrm{dy}} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{3}}{\mathrm{2}}\sqrt{\mathrm{y}}\:\mathrm{e}^{−\mathrm{y}^{\mathrm{3}} } \mathrm{dy}=\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dt}=\frac{\mathrm{2}}{\mathrm{3}}.\frac{\sqrt{\pi}}{\mathrm{2}}=\frac{\sqrt{\pi}}{\mathrm{3}} \\ $$

Commented by PRITHWISH SEN 2 last updated on 08/Aug/20

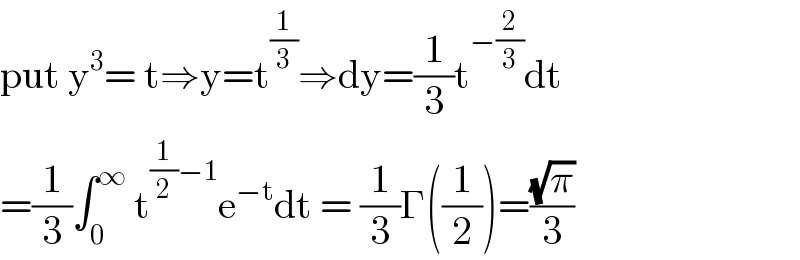
put y^3 = t⇒y=t^(1/3) ⇒dy=(1/3)t^(−(2/3)) dt =(1/3)∫_0 ^∞ t^((1/2)−1) e^(−t) dt = (1/3)Γ((1/2))=((√π)/3)

$$\mathrm{put}\:\mathrm{y}^{\mathrm{3}} =\:\mathrm{t}\Rightarrow\mathrm{y}=\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{3}}} \Rightarrow\mathrm{dy}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{t}^{−\frac{\mathrm{2}}{\mathrm{3}}} \mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \mathrm{e}^{−\mathrm{t}} \mathrm{dt}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\sqrt{\pi}}{\mathrm{3}} \\ $$

Answered by mathmax by abdo last updated on 08/Aug/20

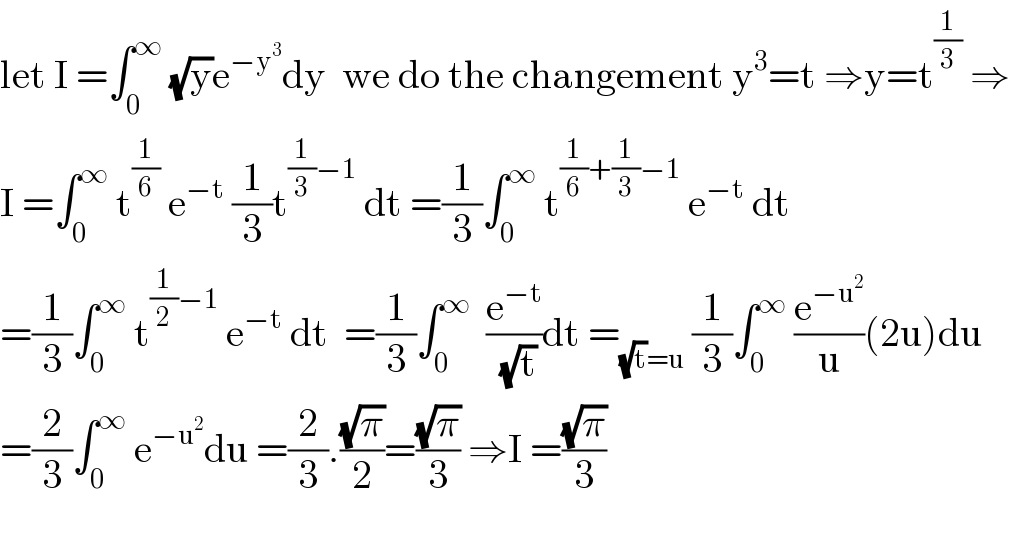
let I =∫_0 ^∞ (√y)e^(−y^3 ) dy we do the changement y^3 =t ⇒y=t^(1/3) ⇒ I =∫_0 ^∞ t^(1/6) e^(−t) (1/3)t^((1/3)−1) dt =(1/3)∫_0 ^∞ t^((1/6)+(1/3)−1) e^(−t) dt =(1/3)∫_0 ^∞ t^((1/2)−1) e^(−t) dt =(1/3)∫_0 ^∞ (e^(−t) /( (√t)))dt =_((√t)=u) (1/3)∫_0 ^∞ (e^(−u^2 ) /u)(2u)du =(2/3)∫_0 ^∞ e^(−u^2 ) du =(2/3).((√π)/2)=((√π)/3) ⇒I =((√π)/3)

$$\mathrm{let}\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\sqrt{\mathrm{y}}\mathrm{e}^{−\mathrm{y}^{\mathrm{3}} } \mathrm{dy}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{y}^{\mathrm{3}} =\mathrm{t}\:\Rightarrow\mathrm{y}=\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{3}}} \:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{6}}} \:\mathrm{e}^{−\mathrm{t}} \:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} \:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\:\:=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{t}} }{\:\sqrt{\mathrm{t}}}\mathrm{dt}\:=_{\sqrt{\mathrm{t}}=\mathrm{u}} \:\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{u}^{\mathrm{2}} } }{\mathrm{u}}\left(\mathrm{2u}\right)\mathrm{du} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{u}^{\mathrm{2}} } \mathrm{du}\:=\frac{\mathrm{2}}{\mathrm{3}}.\frac{\sqrt{\pi}}{\mathrm{2}}=\frac{\sqrt{\pi}}{\mathrm{3}}\:\Rightarrow\mathrm{I}\:=\frac{\sqrt{\pi}}{\mathrm{3}} \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply