Menu Close

Question-107117

Tinku Tara 0 Comments
Pin




Question Number 107117 by Algoritm last updated on 08/Aug/20
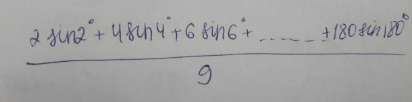
Answered by mr W last updated on 08/Aug/20
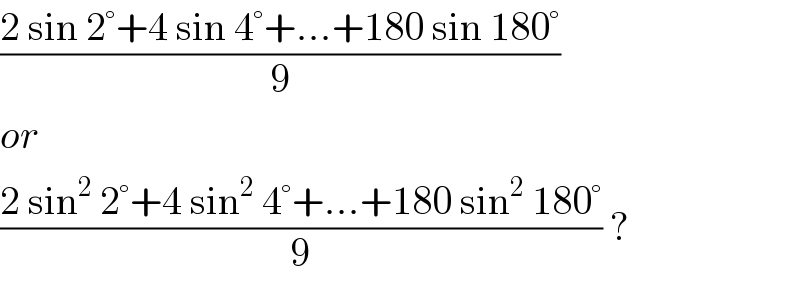
((2 sin 2°+4 sin 4°+...+180 sin 180°)/9) or ((2 sin^2 2°+4 sin^2 4°+...+180 sin^2 180°)/9) ?
$$\frac{\mathrm{2}\:\mathrm{sin}\:\mathrm{2}°+\mathrm{4}\:\mathrm{sin}\:\mathrm{4}°+…+\mathrm{180}\:\mathrm{sin}\:\mathrm{180}°}{\mathrm{9}} \\ $$$${or} \\ $$$$\frac{\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}°+\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{4}°+…+\mathrm{180}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{180}°}{\mathrm{9}}\:? \\ $$
Commented by Algoritm last updated on 08/Aug/20
2sin2°
$$\mathrm{2sin2}° \\ $$
Commented by mr W last updated on 08/Aug/20
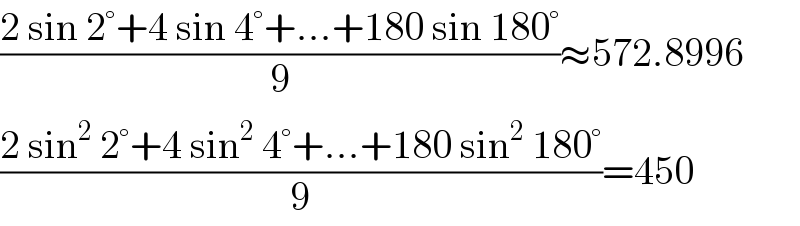
((2 sin 2°+4 sin 4°+...+180 sin 180°)/9)≈572.8996 ((2 sin^2 2°+4 sin^2 4°+...+180 sin^2 180°)/9)=450
$$\frac{\mathrm{2}\:\mathrm{sin}\:\mathrm{2}°+\mathrm{4}\:\mathrm{sin}\:\mathrm{4}°+…+\mathrm{180}\:\mathrm{sin}\:\mathrm{180}°}{\mathrm{9}}\approx\mathrm{572}.\mathrm{8996} \\ $$$$\frac{\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}°+\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{4}°+…+\mathrm{180}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{180}°}{\mathrm{9}}=\mathrm{450} \\ $$
Answered by mathmax by abdo last updated on 08/Aug/20
let S =((2sin(2^o )+4sin(4^o )+....+180sin(180^o ))/9) ⇒ S =(1/9)Σ_(k=1) ^(90) 2ksin(2k^o ) but2 k^(o ) =2((kπ)/(180)) =((kπ)/(90))(radian) ⇒ S =(2/9)Σ_(k=0) ^(90) k sin(((kπ)/(90))) =(2/9) Im(Σ_(k=0) ^(90) k e^(i(((kπ)/(90)))) ) let S_n =Σ_(k=0) ^n k (e^((iπ)/(90)) )^k =f(e^((iπ)/(90)) ) with f(x) =Σ_(k=0) ^n k x^k we have Σ_(k=0) ^n x^k =((x^(n+1) −1)/(x−1)) (x≠1) ⇒Σ_(k=1) ^n kx^(k−1) =((nx^(n+1) −(n+1)x^n +1)/((x−1)^2 )) ⇒Σ_(k=1) ^n kx^k =(x/((1−x)^2 )){ nx^(n+1) −(n+1)x^n +1} ⇒ Σ_(k=0) ^n k(e^((iπ)/(90)) )^k =(e^((iπ)/(90)) /((1−e^((iπ)/(90)) )^2 )){ n(e^((iπ)/(90)) )^(n+1) −(n+1)(e^((iπ)/(90)) )^n +1} ⇒ Σ_(k=0) ^(90) k(e^((iπ)/(90)) )^k =(e^((iπ)/(90)) /((1−cos((π/(90)))−isin((π/(90))))^2 )){ 90e^(i((91)/(90))π) +(91)+1} =((e^((iπ)/(90)) (1−cos((π/(90)))+isin((π/(90))))^2 )/((1−cos((π/(90)))^2 +sin^2 ((π/(90))))){ 90 cos(((91π)/(90)))+i90 sin(((91π)/(90)))+92} rest to extract im(of this quantity)....be continued...
$$\mathrm{let}\:\:\mathrm{S}\:=\frac{\mathrm{2sin}\left(\mathrm{2}^{\mathrm{o}} \right)+\mathrm{4sin}\left(\mathrm{4}^{\mathrm{o}} \right)+….+\mathrm{180sin}\left(\mathrm{180}^{\mathrm{o}} \right)}{\mathrm{9}}\:\Rightarrow \\ $$$$\mathrm{S}\:=\frac{\mathrm{1}}{\mathrm{9}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{90}} \mathrm{2ksin}\left(\mathrm{2k}^{\mathrm{o}} \right)\:\:\:\mathrm{but2}\:\mathrm{k}^{\mathrm{o}\:} \:=\mathrm{2}\frac{\mathrm{k}\pi}{\mathrm{180}}\:=\frac{\mathrm{k}\pi}{\mathrm{90}}\left(\mathrm{radian}\right)\:\Rightarrow \\ $$$$\mathrm{S}\:=\frac{\mathrm{2}}{\mathrm{9}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{90}} \:\mathrm{k}\:\mathrm{sin}\left(\frac{\mathrm{k}\pi}{\mathrm{90}}\right)\:=\frac{\mathrm{2}}{\mathrm{9}}\:\mathrm{Im}\left(\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{90}} \:\mathrm{k}\:\mathrm{e}^{\mathrm{i}\left(\frac{\mathrm{k}\pi}{\mathrm{90}}\right)} \right) \\ $$$$\mathrm{let}\:\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{k}\:\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{90}}} \right)^{\mathrm{k}} \:=\mathrm{f}\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{90}}} \right)\:\mathrm{with}\:\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{k}\:\mathrm{x}^{\mathrm{k}} \:\mathrm{we}\:\mathrm{have} \\ $$$$\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{x}^{\mathrm{k}} \:=\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{x}−\mathrm{1}}\:\:\:\:\left(\mathrm{x}\neq\mathrm{1}\right)\:\Rightarrow\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{kx}^{\mathrm{k}−\mathrm{1}} \:=\frac{\mathrm{nx}^{\mathrm{n}+\mathrm{1}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}} \:+\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{kx}^{\mathrm{k}} \:=\frac{\mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\left\{\:\mathrm{nx}^{\mathrm{n}+\mathrm{1}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}} \:+\mathrm{1}\right\}\:\Rightarrow \\ $$$$\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{k}\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{90}}} \right)^{\mathrm{k}} \:=\frac{\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{90}}} }{\left(\mathrm{1}−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{90}}} \right)^{\mathrm{2}} }\left\{\:\mathrm{n}\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{90}}} \right)^{\mathrm{n}+\mathrm{1}} −\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{90}}} \right)^{\mathrm{n}} \:+\mathrm{1}\right\}\:\Rightarrow \\ $$$$\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{90}} \:\mathrm{k}\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{90}}} \right)^{\mathrm{k}} \:=\frac{\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{90}}} }{\left(\mathrm{1}−\mathrm{cos}\left(\frac{\pi}{\mathrm{90}}\right)−\mathrm{isin}\left(\frac{\pi}{\mathrm{90}}\right)\right)^{\mathrm{2}} }\left\{\:\mathrm{90e}^{\mathrm{i}\frac{\mathrm{91}}{\mathrm{90}}\pi} +\left(\mathrm{91}\right)+\mathrm{1}\right\} \\ $$$$=\frac{\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{90}}} \left(\mathrm{1}−\mathrm{cos}\left(\frac{\pi}{\mathrm{90}}\right)+\mathrm{isin}\left(\frac{\pi}{\mathrm{90}}\right)\right)^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{cos}\left(\frac{\pi}{\mathrm{90}}\right)^{\mathrm{2}} \:+\mathrm{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{90}}\right)\right.}\left\{\:\:\mathrm{90}\:\mathrm{cos}\left(\frac{\mathrm{91}\pi}{\mathrm{90}}\right)+\mathrm{i90}\:\mathrm{sin}\left(\frac{\mathrm{91}\pi}{\mathrm{90}}\right)+\mathrm{92}\right\} \\ $$$$\mathrm{rest}\:\mathrm{to}\:\mathrm{extract}\:\mathrm{im}\left(\mathrm{of}\:\mathrm{this}\:\mathrm{quantity}\right)….\mathrm{be}\:\mathrm{continued}… \\ $$
Commented by Algoritm last updated on 09/Aug/20
thanks
$$\mathrm{thanks} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *