Menu Close

Question-107155

Tinku Tara 0 Comments
Pin




Question Number 107155 by ZiYangLee last updated on 09/Aug/20
Answered by mr W last updated on 09/Aug/20
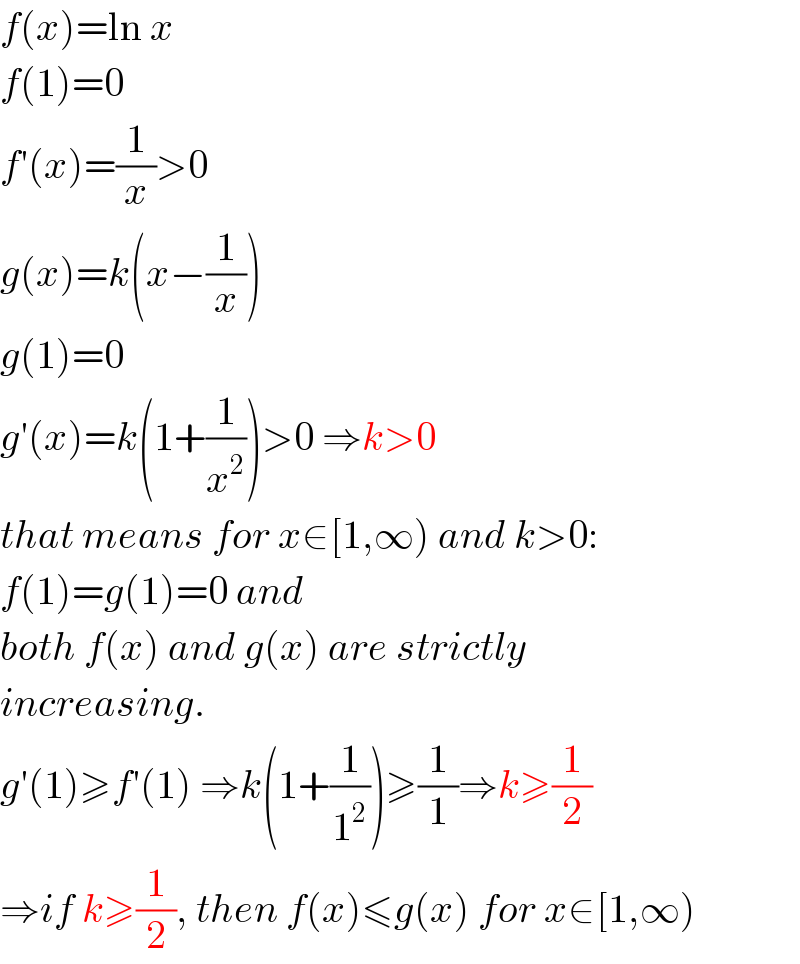
f(x)=ln x f(1)=0 f′(x)=(1/x)>0 g(x)=k(x−(1/x)) g(1)=0 g′(x)=k(1+(1/x^2 ))>0 ⇒k>0 that means for x∈[1,∞) and k>0: f(1)=g(1)=0 and both f(x) and g(x) are strictly increasing. g′(1)≥f′(1) ⇒k(1+(1/1^2 ))≥(1/1)⇒k≥(1/2) ⇒if k≥(1/2), then f(x)≤g(x) for x∈[1,∞)
$${f}\left({x}\right)=\mathrm{ln}\:{x} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$${f}'\left({x}\right)=\frac{\mathrm{1}}{{x}}>\mathrm{0} \\ $$$${g}\left({x}\right)={k}\left({x}−\frac{\mathrm{1}}{{x}}\right) \\ $$$${g}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$${g}'\left({x}\right)={k}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)>\mathrm{0}\:\Rightarrow{k}>\mathrm{0} \\ $$$${that}\:{means}\:{for}\:{x}\in\left[\mathrm{1},\infty\right)\:{and}\:{k}>\mathrm{0}: \\ $$$${f}\left(\mathrm{1}\right)={g}\left(\mathrm{1}\right)=\mathrm{0}\:{and} \\ $$$${both}\:{f}\left({x}\right)\:{and}\:{g}\left({x}\right)\:{are}\:{strictly} \\ $$$${increasing}. \\ $$$${g}'\left(\mathrm{1}\right)\geqslant{f}'\left(\mathrm{1}\right)\:\Rightarrow{k}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }\right)\geqslant\frac{\mathrm{1}}{\mathrm{1}}\Rightarrow{k}\geqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{if}\:{k}\geqslant\frac{\mathrm{1}}{\mathrm{2}},\:{then}\:{f}\left({x}\right)\leqslant{g}\left({x}\right)\:{for}\:{x}\in\left[\mathrm{1},\infty\right) \\ $$
Commented by ZiYangLee last updated on 09/Aug/20
thanksss
$$\mathrm{thanksss} \\ $$
Commented by ZiYangLee last updated on 09/Aug/20
But special case cannot prove general case unless you can ensure that there is no loss of generality. hmmmmm
$$\mathrm{But}\:\mathrm{special}\:\mathrm{case}\:\mathrm{cannot}\:\mathrm{prove}\:\mathrm{general} \\ $$$$\mathrm{case}\:\mathrm{unless}\:\mathrm{you}\:\mathrm{can}\:\mathrm{ensure}\:\mathrm{that}\:\mathrm{there} \\ $$$$\mathrm{is}\:\mathrm{no}\:\mathrm{loss}\:\mathrm{of}\:\mathrm{generality}.\:\mathrm{hmmmmm} \\ $$
Commented by mr W last updated on 09/Aug/20
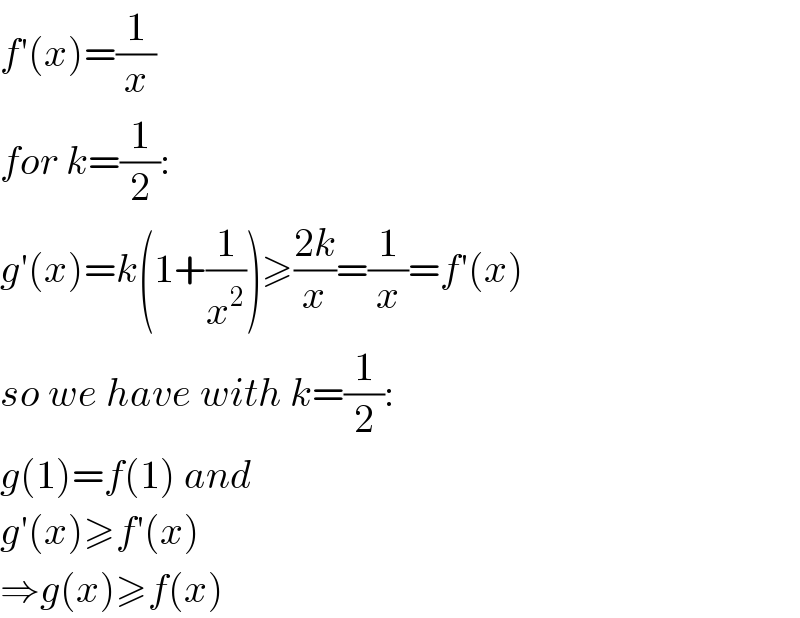
f′(x)=(1/x) for k=(1/2): g′(x)=k(1+(1/x^2 ))≥((2k)/x)=(1/x)=f′(x) so we have with k=(1/2): g(1)=f(1) and g′(x)≥f′(x) ⇒g(x)≥f(x)
$${f}'\left({x}\right)=\frac{\mathrm{1}}{{x}} \\ $$$${for}\:{k}=\frac{\mathrm{1}}{\mathrm{2}}: \\ $$$${g}'\left({x}\right)={k}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\geqslant\frac{\mathrm{2}{k}}{{x}}=\frac{\mathrm{1}}{{x}}={f}'\left({x}\right) \\ $$$${so}\:{we}\:{have}\:{with}\:{k}=\frac{\mathrm{1}}{\mathrm{2}}: \\ $$$${g}\left(\mathrm{1}\right)={f}\left(\mathrm{1}\right)\:{and} \\ $$$${g}'\left({x}\right)\geqslant{f}'\left({x}\right) \\ $$$$\Rightarrow{g}\left({x}\right)\geqslant{f}\left({x}\right) \\ $$
Answered by 1549442205PVT last updated on 09/Aug/20
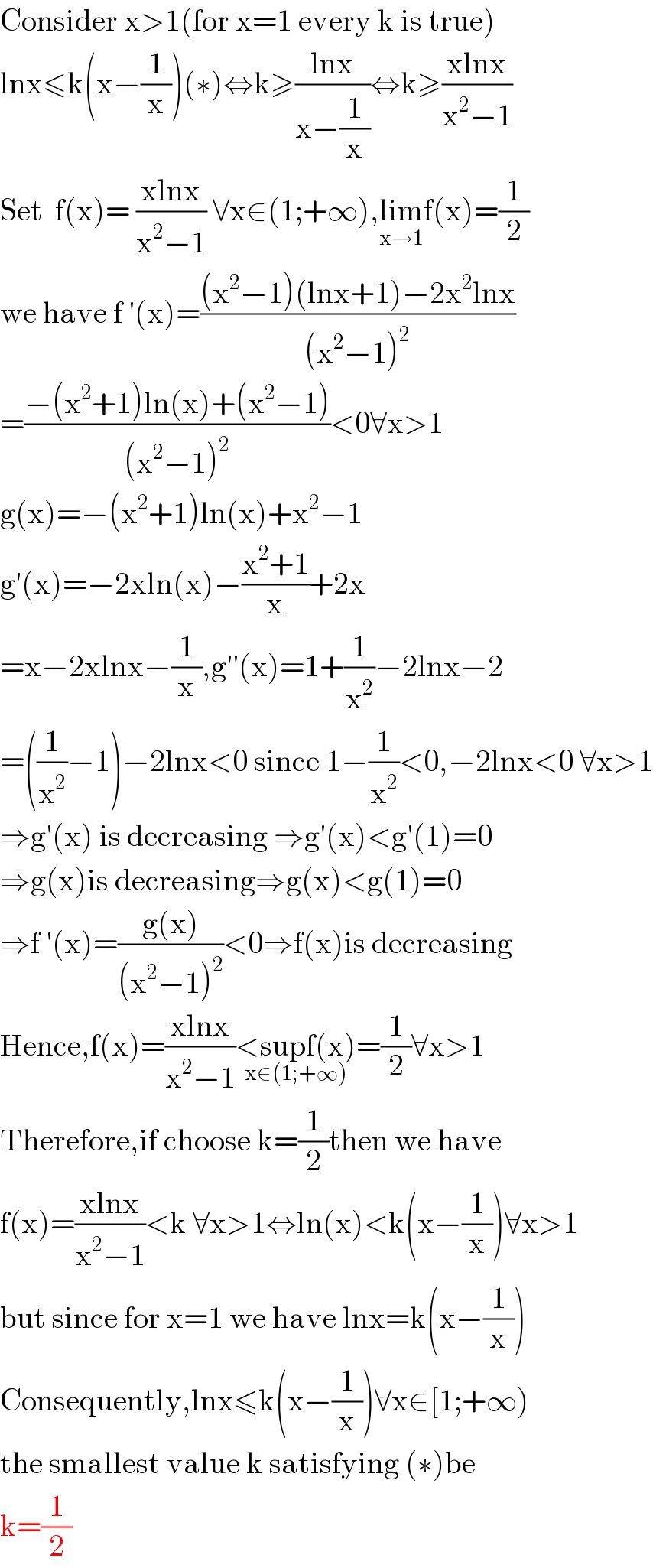
Consider x>1(for x=1 every k is true) lnx≤k(x−(1/x))(∗)⇔k≥((lnx)/(x−(1/x)))⇔k≥((xlnx)/(x^2 −1)) Set f(x)= ((xlnx)/(x^2 −1)) ∀x∈(1;+∞),lim_(x→1) f(x)=(1/2) we have f ′(x)=(((x^2 −1)(lnx+1)−2x^2 lnx)/((x^2 −1)^2 )) =((−(x^2 +1)ln(x)+(x^2 −1))/((x^2 −1)^2 ))<0∀x>1 g(x)=−(x^2 +1)ln(x)+x^2 −1 g′(x)=−2xln(x)−((x^2 +1)/x)+2x =x−2xlnx−(1/x),g′′(x)=1+(1/x^2 )−2lnx−2 =((1/x^2 )−1)−2lnx<0 since 1−(1/x^2 )<0,−2lnx<0 ∀x>1 ⇒g′(x) is decreasing ⇒g′(x)<g′(1)=0 ⇒g(x)is decreasing⇒g(x)<g(1)=0 ⇒f ′(x)=((g(x))/((x^2 −1)^2 ))<0⇒f(x)is decreasing Hence,f(x)=((xlnx)/(x^2 −1))<supf(x)_(x∈(1;+∞)) =(1/2)∀x>1 Therefore,if choose k=(1/2)then we have f(x)=((xlnx)/(x^2 −1))<k ∀x>1⇔ln(x)<k(x−(1/x))∀x>1 but since for x=1 we have lnx=k(x−(1/x)) Consequently,lnx≤k(x−(1/x))∀x∈[1;+∞) the smallest value k satisfying (∗)be k=(1/2)
$$\mathrm{Consider}\:\mathrm{x}>\mathrm{1}\left(\mathrm{for}\:\mathrm{x}=\mathrm{1}\:\mathrm{every}\:\mathrm{k}\:\mathrm{is}\:\mathrm{true}\right) \\ $$$$\mathrm{lnx}\leqslant\mathrm{k}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)\left(\ast\right)\Leftrightarrow\mathrm{k}\geqslant\frac{\mathrm{lnx}}{\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}}\Leftrightarrow\mathrm{k}\geqslant\frac{\mathrm{xlnx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\mathrm{Set}\:\:\mathrm{f}\left(\mathrm{x}\right)=\:\frac{\mathrm{xlnx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:\forall\mathrm{x}\in\left(\mathrm{1};+\infty\right),\underset{\mathrm{x}\rightarrow\mathrm{1}} {\mathrm{lim}f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{f}\:'\left(\mathrm{x}\right)=\frac{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{lnx}+\mathrm{1}\right)−\mathrm{2x}^{\mathrm{2}} \mathrm{lnx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{−\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{ln}\left(\mathrm{x}\right)+\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }<\mathrm{0}\forall\mathrm{x}>\mathrm{1} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=−\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{ln}\left(\mathrm{x}\right)+\mathrm{x}^{\mathrm{2}} −\mathrm{1} \\ $$$$\mathrm{g}'\left(\mathrm{x}\right)=−\mathrm{2xln}\left(\mathrm{x}\right)−\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{x}}+\mathrm{2x} \\ $$$$=\mathrm{x}−\mathrm{2xlnx}−\frac{\mathrm{1}}{\mathrm{x}},\mathrm{g}''\left(\mathrm{x}\right)=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{2lnx}−\mathrm{2} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{1}\right)−\mathrm{2lnx}<\mathrm{0}\:\mathrm{since}\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }<\mathrm{0},−\mathrm{2lnx}<\mathrm{0}\:\forall\mathrm{x}>\mathrm{1} \\ $$$$\Rightarrow\mathrm{g}'\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{decreasing}\:\Rightarrow\mathrm{g}'\left(\mathrm{x}\right)<\mathrm{g}'\left(\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{g}\left(\mathrm{x}\right)\mathrm{is}\:\mathrm{decreasing}\Rightarrow\mathrm{g}\left(\mathrm{x}\right)<\mathrm{g}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{f}\:'\left(\mathrm{x}\right)=\frac{\mathrm{g}\left(\mathrm{x}\right)}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }<\mathrm{0}\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\mathrm{is}\:\mathrm{decreasing} \\ $$$$\mathrm{Hence},\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{xlnx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\underset{\mathrm{x}\in\left(\mathrm{1};+\infty\right)} {<\mathrm{supf}\left(\mathrm{x}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\forall\mathrm{x}>\mathrm{1} \\ $$$$\mathrm{Therefore},\mathrm{if}\:\mathrm{choose}\:\mathrm{k}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{then}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{xlnx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}<\mathrm{k}\:\forall\mathrm{x}>\mathrm{1}\Leftrightarrow\mathrm{ln}\left(\mathrm{x}\right)<\mathrm{k}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)\forall\mathrm{x}>\mathrm{1} \\ $$$$\mathrm{but}\:\mathrm{since}\:\mathrm{for}\:\mathrm{x}=\mathrm{1}\:\mathrm{we}\:\mathrm{have}\:\mathrm{lnx}=\mathrm{k}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$\mathrm{Consequently},\mathrm{lnx}\leqslant\mathrm{k}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)\forall\mathrm{x}\in\left[\mathrm{1};+\infty\right) \\ $$$$\mathrm{the}\:\mathrm{smallest}\:\mathrm{value}\:\mathrm{k}\:\mathrm{satisfying}\:\left(\ast\right)\mathrm{be} \\ $$$$\mathrm{k}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by 1549442205PVT last updated on 09/Aug/20
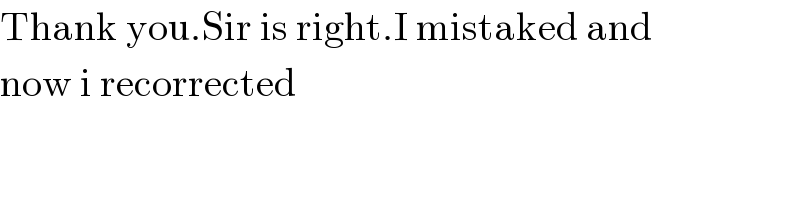
Thank you.Sir is right.I mistaked and now i recorrected
$$\mathrm{Thank}\:\mathrm{you}.\mathrm{Sir}\:\mathrm{is}\:\mathrm{right}.\mathrm{I}\:\mathrm{mistaked}\:\mathrm{and} \\ $$$$\mathrm{now}\:\mathrm{i}\:\mathrm{recorrected}\: \\ $$
Commented by mr W last updated on 09/Aug/20
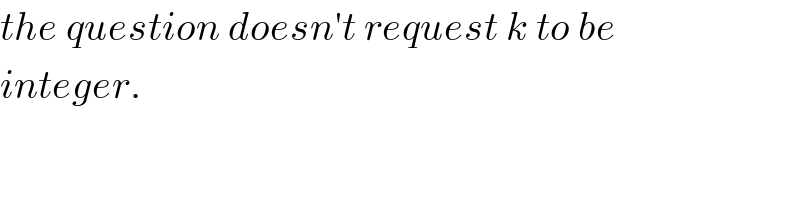
the question doesn′t request k to be integer.
$${the}\:{question}\:{doesn}'{t}\:{request}\:{k}\:{to}\:{be} \\ $$$${integer}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *