Question Number 107178 by 175mohamed last updated on 09/Aug/20
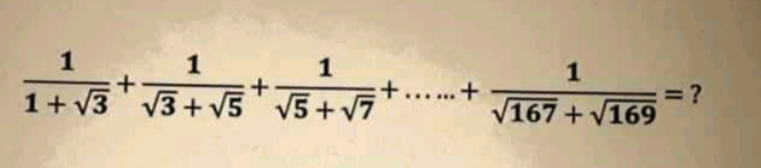
Commented by mr W last updated on 09/Aug/20
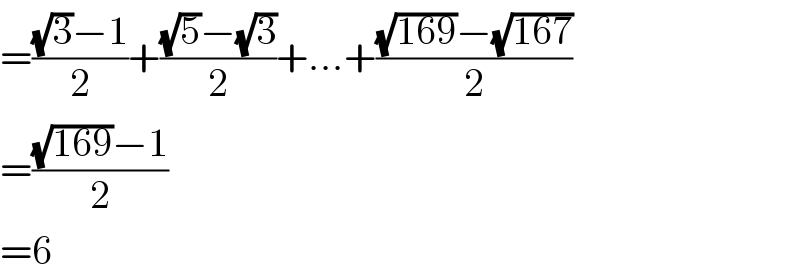
$$=\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}−\sqrt{\mathrm{3}}}{\mathrm{2}}+…+\frac{\sqrt{\mathrm{169}}−\sqrt{\mathrm{167}}}{\mathrm{2}} \\ $$$$=\frac{\sqrt{\mathrm{169}}−\mathrm{1}}{\mathrm{2}} \\ $$$$=\mathrm{6} \\ $$
Answered by Dwaipayan Shikari last updated on 09/Aug/20

$$\mathrm{First}\:\mathrm{term} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{3}}}=\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{2nd}\:\mathrm{term}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}+\sqrt{\mathrm{5}}}=\frac{\sqrt{\mathrm{5}}−\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$… \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{167}}+\sqrt{\mathrm{169}}}=\frac{\sqrt{\mathrm{169}}−\sqrt{\mathrm{167}}}{\mathrm{2}} \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+….\frac{\sqrt{\mathrm{167}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{165}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{169}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{167}}}{\mathrm{2}} \\ $$$$=\mathrm{6} \\ $$$$ \\ $$
