Question Number 107446 by mathdave last updated on 10/Aug/20

Commented by kaivan.ahmadi last updated on 10/Aug/20
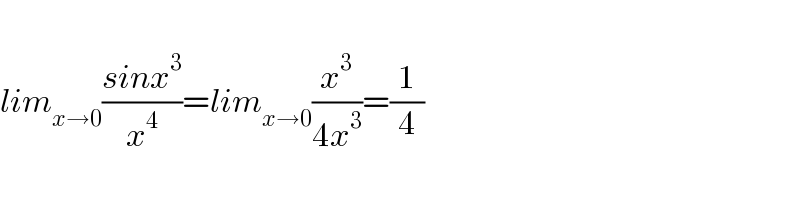
$$ \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \frac{{sinx}^{\mathrm{3}} }{{x}^{\mathrm{4}} }={lim}_{{x}\rightarrow\mathrm{0}} \frac{{x}^{\mathrm{3}} }{\mathrm{4}{x}^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by mr W last updated on 10/Aug/20

$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{x}^{\mathrm{3}} }{\mathrm{4}{x}^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by mr W last updated on 10/Aug/20
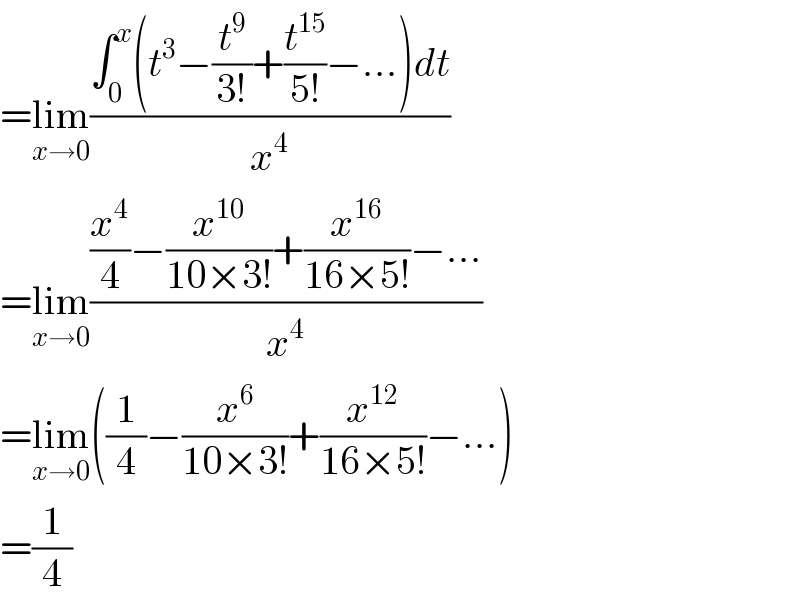
$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\int_{\mathrm{0}} ^{{x}} \left({t}^{\mathrm{3}} −\frac{{t}^{\mathrm{9}} }{\mathrm{3}!}+\frac{{t}^{\mathrm{15}} }{\mathrm{5}!}−…\right){dt}}{{x}^{\mathrm{4}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{x}^{\mathrm{4}} }{\mathrm{4}}−\frac{{x}^{\mathrm{10}} }{\mathrm{10}×\mathrm{3}!}+\frac{{x}^{\mathrm{16}} }{\mathrm{16}×\mathrm{5}!}−…}{{x}^{\mathrm{4}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{4}}−\frac{{x}^{\mathrm{6}} }{\mathrm{10}×\mathrm{3}!}+\frac{{x}^{\mathrm{12}} }{\mathrm{16}×\mathrm{5}!}−…\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
