Menu Close

Question-107547

Tinku Tara 0 Comments
Pin




Question Number 107547 by hgrocks last updated on 11/Aug/20
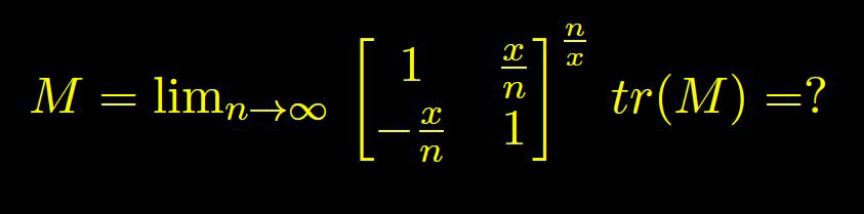
Commented by hgrocks last updated on 11/Aug/20
Can anyone solve this Q without using eigen values
Commented by bemath last updated on 11/Aug/20
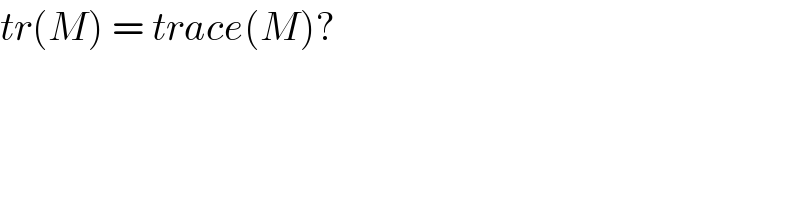
tr(M) = trace(M)?
$${tr}\left({M}\right)\:=\:{trace}\left({M}\right)? \\ $$
Commented by hgrocks last updated on 11/Aug/20
Yes it is trace of M
Commented by hgrocks last updated on 11/Aug/20
Pls Solve This Q
$$\mathrm{Pls}\:\mathrm{Solve}\:\mathrm{This}\:\mathrm{Q} \\ $$
Commented by hgrocks last updated on 11/Aug/20
Anyone?
$$\mathrm{Anyone}?\: \\ $$$$ \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 11/Aug/20
sir dont beg the answer if someone have a idea he give it...
$$\mathrm{sir}\:\mathrm{dont}\:\mathrm{beg}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{if}\:\mathrm{someone}\:\mathrm{have}\:\mathrm{a}\:\mathrm{idea}\:\mathrm{he}\:\mathrm{give}\:\mathrm{it}… \\ $$
Answered by mathmax by abdo last updated on 12/Aug/20
let take a try with this limit let A_n = (((1 (x/n))),((−(x/n) 1)) ) we have A_n =(√(1+(x^2 /n^2 )))× ((((1/( (√(1+(x^2 /n^2 ))))) (x/(n(√(1+(x^2 /n^2 ))))))),((−(x/(n(√(1+(x^2 /n^2 ))))) (1/( (√(1+(x^2 /n^2 ))))))) ) let α_n (x) =(√(1+(x^2 /n^2 ))) ⇒A_n =α_n (x) ((((1/(α_n (x))) (x/(nα_n (x))))),((−(x/(nα_n (x))) (1/(α_n (x))))) ) we have det (((......)),() )=(1/(α_n ^2 (x))) +(x^2 /(n^2 α_n ^2 (x))) =(1/(1+(x^2 /n^2 ))) +(x^2 /(n^2 (1+(x^2 /n^2 )))) =(n^2 /(n^2 +x^2 )) +(x^2 /(n^2 +x^2 )) =1 let (1/(α_n (x))) =cosα and (x/(nα_n (x))) =sin(α) ⇒ tanα =(x/n) ⇒ α =arctan((x/n)) ⇒ A_n ^(n/x) =α_n (x))^(n/x) × ((( cosα sinα)),((−sinα cosα)) )^(n/x) =(1+(x^2 /n^2 ))^(n/(2x)) × (((cosα sinα)),((−sinα cosα)) )^(n/x) if x divide n we get A_n ^(n/x) =(1+(x^2 /n^2 ))^(n/(2x)) (((cos((n/x)arctan((x/n))) sin((n/x)arctan((x/n))))),((−sin((n/x)arctan((x/n))) cos((n/x)arctan((x/n))))) ) (1+(x^2 /n^2 ))^(n/(2x)) =e^((n/(2x))ln(1+(x^2 /n^2 ))) ∼e^((n/(2x))((x^2 /n^2 ))) =e^(x/(2n)) →1 also (n/x)arctan((x/n)) ∼(n/x).(x/n) =1 ⇒lim_(n→+∞) A_n ^(n/x) = (((cos(1) sin(1))),((−sin(1) cos(1))) ) and Tr(lim_(n→+∞) A_n ^(n/x) ) =2cos(1) if n integr and x dont divide n n =qx +p with 0<p<x be continued...
$$\mathrm{let}\:\mathrm{take}\:\mathrm{a}\:\mathrm{try}\:\mathrm{with}\:\mathrm{this}\:\mathrm{limit}\:\mathrm{let}\:\mathrm{A}_{\mathrm{n}} =\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{x}}{\mathrm{n}}}\\{−\frac{\mathrm{x}}{\mathrm{n}}\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{A}_{\mathrm{n}} =\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }}×\begin{pmatrix}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{x}}{\mathrm{n}\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }}}}\\{−\frac{\mathrm{x}}{\mathrm{n}\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }}}}\end{pmatrix} \\ $$$$\mathrm{let}\:\:\alpha_{\mathrm{n}} \left(\mathrm{x}\right)\:=\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }}\:\Rightarrow\mathrm{A}_{\mathrm{n}} =\alpha_{\mathrm{n}} \left(\mathrm{x}\right)\begin{pmatrix}{\frac{\mathrm{1}}{\alpha_{\mathrm{n}} \left(\mathrm{x}\right)}\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{x}}{\mathrm{n}\alpha_{\mathrm{n}} \left(\mathrm{x}\right)}}\\{−\frac{\mathrm{x}}{\mathrm{n}\alpha_{\mathrm{n}} \left(\mathrm{x}\right)}\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\alpha_{\mathrm{n}} \left(\mathrm{x}\right)}}\end{pmatrix} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{det}\begin{pmatrix}{……}\\{}\end{pmatrix}=\frac{\mathrm{1}}{\alpha_{\mathrm{n}} ^{\mathrm{2}} \left(\mathrm{x}\right)}\:+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} \alpha_{\mathrm{n}} ^{\mathrm{2}} \left(\mathrm{x}\right)}\:=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }}\:+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }\right)} \\ $$$$=\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} \:+\mathrm{x}^{\mathrm{2}} }\:+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} \:+\mathrm{x}^{\mathrm{2}} }\:=\mathrm{1}\:\:\:\mathrm{let}\:\frac{\mathrm{1}}{\alpha_{\mathrm{n}} \left(\mathrm{x}\right)}\:=\mathrm{cos}\alpha\:\:\mathrm{and}\:\frac{\mathrm{x}}{\mathrm{n}\alpha_{\mathrm{n}} \left(\mathrm{x}\right)}\:=\mathrm{sin}\left(\alpha\right)\:\Rightarrow \\ $$$$\mathrm{tan}\alpha\:=\frac{\mathrm{x}}{\mathrm{n}}\:\Rightarrow\:\alpha\:=\mathrm{arctan}\left(\frac{\mathrm{x}}{\mathrm{n}}\right)\:\Rightarrow \\ $$$$\left.\mathrm{A}_{\mathrm{n}} ^{\frac{\mathrm{n}}{\mathrm{x}}} \:=\alpha_{\mathrm{n}} \left(\mathrm{x}\right)\right)^{\frac{\mathrm{n}}{\mathrm{x}}} \:\:×\begin{pmatrix}{\:\mathrm{cos}\alpha\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{sin}\alpha}\\{−\mathrm{sin}\alpha\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\alpha}\end{pmatrix}^{\frac{\mathrm{n}}{\mathrm{x}}} \\ $$$$=\left(\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }\right)^{\frac{\mathrm{n}}{\mathrm{2x}}} \:×\begin{pmatrix}{\mathrm{cos}\alpha\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{sin}\alpha}\\{−\mathrm{sin}\alpha\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\alpha}\end{pmatrix}^{\frac{\mathrm{n}}{\mathrm{x}}} \:\:\:\mathrm{if}\:\mathrm{x}\:\mathrm{divide}\:\mathrm{n}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{A}_{\mathrm{n}} ^{\frac{\mathrm{n}}{\mathrm{x}}} \:\:\:=\left(\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }\right)^{\frac{\mathrm{n}}{\mathrm{2x}}} \begin{pmatrix}{\mathrm{cos}\left(\frac{\mathrm{n}}{\mathrm{x}}\mathrm{arctan}\left(\frac{\mathrm{x}}{\mathrm{n}}\right)\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{sin}\left(\frac{\mathrm{n}}{\mathrm{x}}\mathrm{arctan}\left(\frac{\mathrm{x}}{\mathrm{n}}\right)\right)}\\{−\mathrm{sin}\left(\frac{\mathrm{n}}{\mathrm{x}}\mathrm{arctan}\left(\frac{\mathrm{x}}{\mathrm{n}}\right)\right)\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\left(\frac{\mathrm{n}}{\mathrm{x}}\mathrm{arctan}\left(\frac{\mathrm{x}}{\mathrm{n}}\right)\right)}\end{pmatrix} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }\right)^{\frac{\mathrm{n}}{\mathrm{2x}}} \:=\mathrm{e}^{\frac{\mathrm{n}}{\mathrm{2x}}\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }\right)} \:\:\sim\mathrm{e}^{\frac{\mathrm{n}}{\mathrm{2x}}\left(\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }\right)} \:=\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2n}}} \:\rightarrow\mathrm{1}\:\:\mathrm{also}\:\frac{\mathrm{n}}{\mathrm{x}}\mathrm{arctan}\left(\frac{\mathrm{x}}{\mathrm{n}}\right) \\ $$$$\sim\frac{\mathrm{n}}{\mathrm{x}}.\frac{\mathrm{x}}{\mathrm{n}}\:=\mathrm{1}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{A}_{\mathrm{n}} ^{\frac{\mathrm{n}}{\mathrm{x}}} \:\:=\begin{pmatrix}{\mathrm{cos}\left(\mathrm{1}\right)\:\:\:\:\:\:\:\:\:\:\mathrm{sin}\left(\mathrm{1}\right)}\\{−\mathrm{sin}\left(\mathrm{1}\right)\:\:\:\:\:\:\:\:\:\mathrm{cos}\left(\mathrm{1}\right)}\end{pmatrix} \\ $$$$\mathrm{and}\:\mathrm{Tr}\left(\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{A}_{\mathrm{n}} ^{\frac{\mathrm{n}}{\mathrm{x}}} \right)\:=\mathrm{2cos}\left(\mathrm{1}\right) \\ $$$$\mathrm{if}\:\mathrm{n}\:\mathrm{integr}\:\mathrm{and}\:\mathrm{x}\:\mathrm{dont}\:\mathrm{divide}\:\:\mathrm{n}\:\:\:\mathrm{n}\:=\mathrm{qx}\:+\mathrm{p}\:\mathrm{with}\:\mathrm{0}<\mathrm{p}<\mathrm{x} \\ $$$$\mathrm{be}\:\mathrm{continued}… \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *