Question Number 107555 by anonymous last updated on 11/Aug/20

Answered by bshahid010 last updated on 11/Aug/20
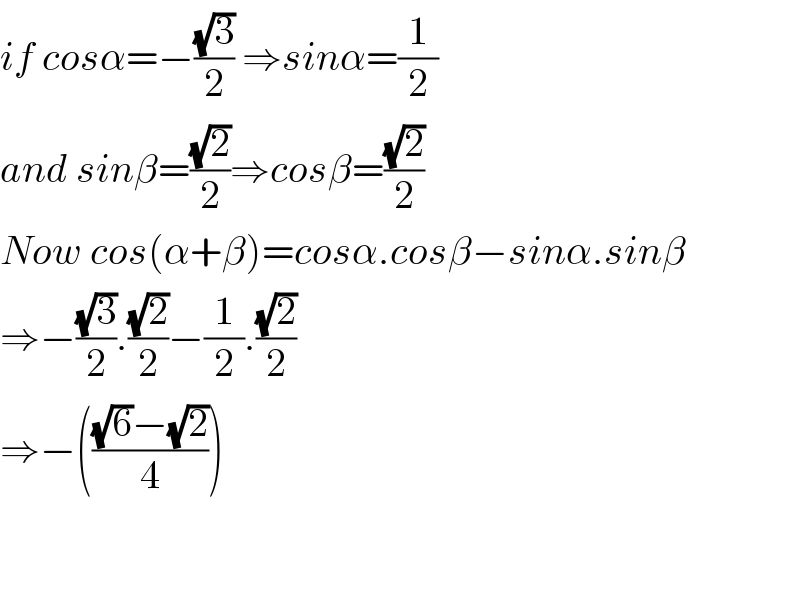
$${if}\:{cos}\alpha=−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Rightarrow{sin}\alpha=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${and}\:{sin}\beta=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\Rightarrow{cos}\beta=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${Now}\:{cos}\left(\alpha+\beta\right)={cos}\alpha.{cos}\beta−{sin}\alpha.{sin}\beta \\ $$$$\Rightarrow−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}.\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\Rightarrow−\left(\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{4}}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by anonymous last updated on 12/Aug/20
thank a lot sir
Answered by bshahid010 last updated on 11/Aug/20
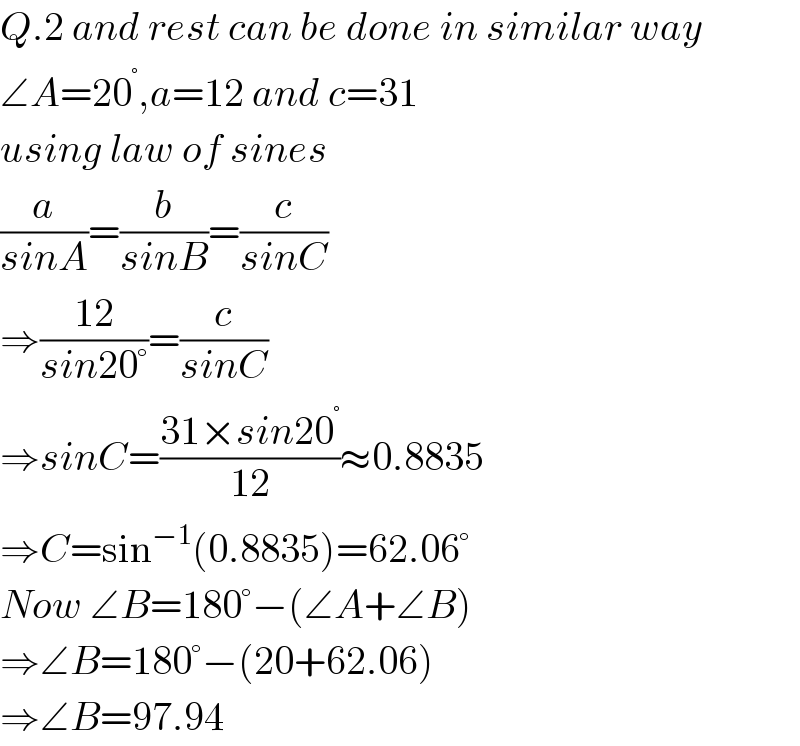
$${Q}.\mathrm{2}\:{and}\:{rest}\:{can}\:{be}\:{done}\:{in}\:{similar}\:{way} \\ $$$$\angle{A}=\mathrm{20}^{°} ,{a}=\mathrm{12}\:{and}\:{c}=\mathrm{31} \\ $$$${using}\:{law}\:{of}\:{sines} \\ $$$$\frac{{a}}{{sinA}}=\frac{{b}}{{sinB}}=\frac{{c}}{{sinC}} \\ $$$$\Rightarrow\frac{\mathrm{12}}{{sin}\mathrm{20}°}=\frac{{c}}{{sinC}} \\ $$$$\Rightarrow{sinC}=\frac{\mathrm{31}×{sin}\mathrm{20}^{°} }{\mathrm{12}}\approx\mathrm{0}.\mathrm{8835} \\ $$$$\Rightarrow{C}=\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{0}.\mathrm{8835}\right)=\mathrm{62}.\mathrm{06}° \\ $$$${Now}\:\angle{B}=\mathrm{180}°−\left(\angle{A}+\angle{B}\right) \\ $$$$\Rightarrow\angle{B}=\mathrm{180}°−\left(\mathrm{20}+\mathrm{62}.\mathrm{06}\right) \\ $$$$\Rightarrow\angle{B}=\mathrm{97}.\mathrm{94} \\ $$
Commented by anonymous last updated on 12/Aug/20
Thank you Sir
