Question Number 107572 by ajfour last updated on 11/Aug/20

Commented by ajfour last updated on 11/Aug/20

$${The}\:{cones}\:{have}\:{base}\:{radius}\:{r}\:{and} \\ $$$${semi}-{vertical}\:{angle}\:\alpha/\mathrm{2}.\:{Find} \\ $$$${radius}\:{of}\:{the}\:{pink}\:{sphere}\:{that} \\ $$$${touches}\:{the}\:{cones}\:{externally}\:{and} \\ $$$${touches}\:{the}\:{plane}\:{passing}\:{through} \\ $$$${the}\:{cone}\:{vertices}. \\ $$
Answered by mr W last updated on 11/Aug/20

Commented by mr W last updated on 11/Aug/20
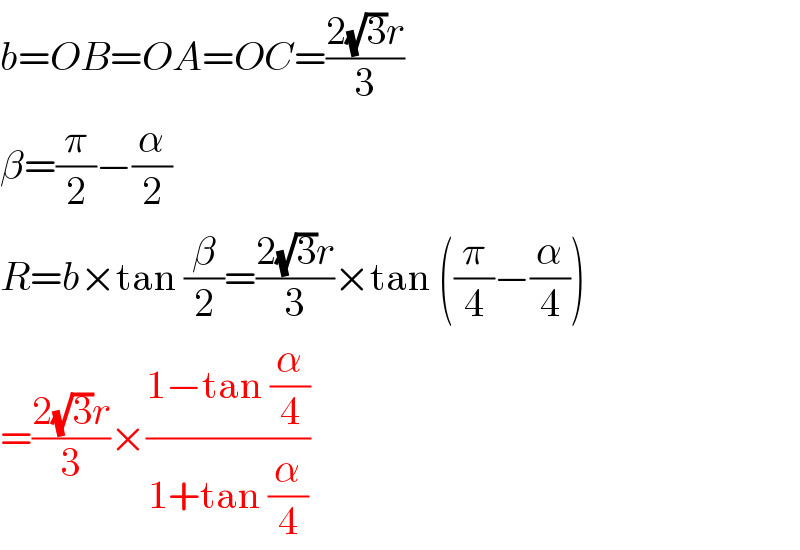
$${b}={OB}={OA}={OC}=\frac{\mathrm{2}\sqrt{\mathrm{3}}{r}}{\mathrm{3}} \\ $$$$\beta=\frac{\pi}{\mathrm{2}}−\frac{\alpha}{\mathrm{2}} \\ $$$${R}={b}×\mathrm{tan}\:\frac{\beta}{\mathrm{2}}=\frac{\mathrm{2}\sqrt{\mathrm{3}}{r}}{\mathrm{3}}×\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\mathrm{4}}\right) \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{3}}{r}}{\mathrm{3}}×\frac{\mathrm{1}−\mathrm{tan}\:\frac{\alpha}{\mathrm{4}}}{\mathrm{1}+\mathrm{tan}\:\frac{\alpha}{\mathrm{4}}} \\ $$
Commented by ajfour last updated on 11/Aug/20
$${Perfect}!\:\:{Thank}\:{you}\:{Sir}. \\ $$
Commented by otchereabdullai@gmail.com last updated on 12/Aug/20

$$\mathrm{fantastic}\:\mathrm{prof} \\ $$
