Menu Close

Question-107589

Tinku Tara 0 Comments
Pin




Question Number 107589 by mathdave last updated on 11/Aug/20
Answered by Ar Brandon last updated on 11/Aug/20
I=∫(((x+6)/(x+8)))^6 dx=∫(1−(2/(x+8)))^6 dx =∫{1−((12)/(x+8))+((60)/((x+8)^2 ))−((160)/((x+8)^3 ))+((240)/((x+8)^4 ))−((192)/((x+8)^5 ))+((64)/((x+8)^6 ))}dx =x−12ln∣x+8∣−((60)/(x+8))+((80)/((x+8)^2 ))−((80)/((x+8)^3 ))+((48)/((x+8)^4 ))−((12,8)/((x+8)^5 ))+C
$$\mathcal{I}=\int\left(\frac{\mathrm{x}+\mathrm{6}}{\mathrm{x}+\mathrm{8}}\right)^{\mathrm{6}} \mathrm{dx}=\int\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{x}+\mathrm{8}}\right)^{\mathrm{6}} \mathrm{dx} \\ $$$$\:\:\:=\int\left\{\mathrm{1}−\frac{\mathrm{12}}{\mathrm{x}+\mathrm{8}}+\frac{\mathrm{60}}{\left(\mathrm{x}+\mathrm{8}\right)^{\mathrm{2}} }−\frac{\mathrm{160}}{\left(\mathrm{x}+\mathrm{8}\right)^{\mathrm{3}} }+\frac{\mathrm{240}}{\left(\mathrm{x}+\mathrm{8}\right)^{\mathrm{4}} }−\frac{\mathrm{192}}{\left(\mathrm{x}+\mathrm{8}\right)^{\mathrm{5}} }+\frac{\mathrm{64}}{\left(\mathrm{x}+\mathrm{8}\right)^{\mathrm{6}} }\right\}\mathrm{dx} \\ $$$$\:\:\:=\mathrm{x}−\mathrm{12ln}\mid\mathrm{x}+\mathrm{8}\mid−\frac{\mathrm{60}}{\mathrm{x}+\mathrm{8}}+\frac{\mathrm{80}}{\left(\mathrm{x}+\mathrm{8}\right)^{\mathrm{2}} }−\frac{\mathrm{80}}{\left(\mathrm{x}+\mathrm{8}\right)^{\mathrm{3}} }+\frac{\mathrm{48}}{\left(\mathrm{x}+\mathrm{8}\right)^{\mathrm{4}} }−\frac{\mathrm{12},\mathrm{8}}{\left(\mathrm{x}+\mathrm{8}\right)^{\mathrm{5}} }+\mathcal{C} \\ $$
Answered by Her_Majesty last updated on 11/Aug/20
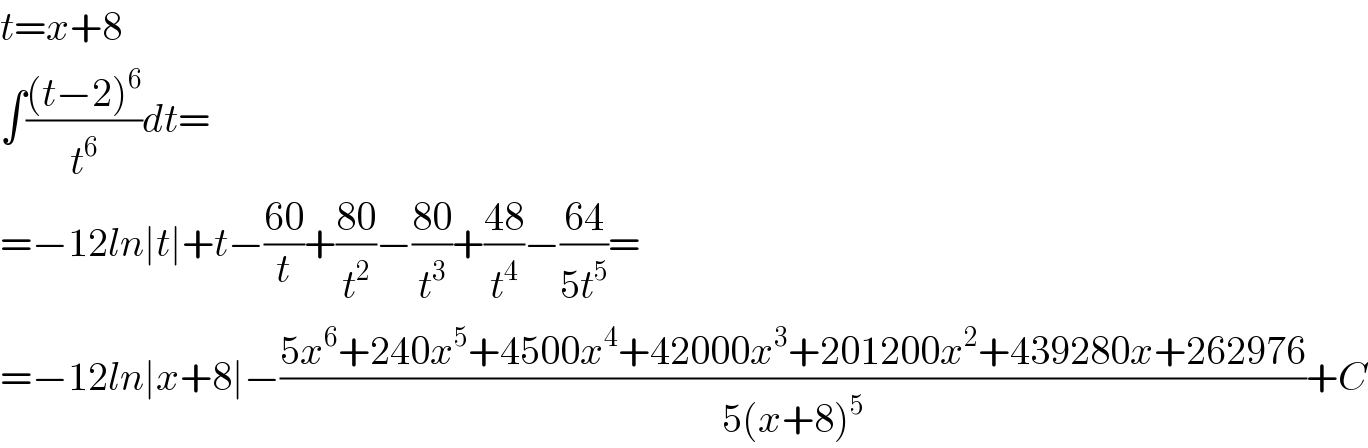
t=x+8 ∫(((t−2)^6 )/t^6 )dt= =−12ln∣t∣+t−((60)/t)+((80)/t^2 )−((80)/t^3 )+((48)/t^4 )−((64)/(5t^5 ))= =−12ln∣x+8∣−((5x^6 +240x^5 +4500x^4 +42000x^3 +201200x^2 +439280x+262976)/(5(x+8)^5 ))+C
$${t}={x}+\mathrm{8} \\ $$$$\int\frac{\left({t}−\mathrm{2}\right)^{\mathrm{6}} }{{t}^{\mathrm{6}} }{dt}= \\ $$$$=−\mathrm{12}{ln}\mid{t}\mid+{t}−\frac{\mathrm{60}}{{t}}+\frac{\mathrm{80}}{{t}^{\mathrm{2}} }−\frac{\mathrm{80}}{{t}^{\mathrm{3}} }+\frac{\mathrm{48}}{{t}^{\mathrm{4}} }−\frac{\mathrm{64}}{\mathrm{5}{t}^{\mathrm{5}} }= \\ $$$$=−\mathrm{12}{ln}\mid{x}+\mathrm{8}\mid−\frac{\mathrm{5}{x}^{\mathrm{6}} +\mathrm{240}{x}^{\mathrm{5}} +\mathrm{4500}{x}^{\mathrm{4}} +\mathrm{42000}{x}^{\mathrm{3}} +\mathrm{201200}{x}^{\mathrm{2}} +\mathrm{439280}{x}+\mathrm{262976}}{\mathrm{5}\left({x}+\mathrm{8}\right)^{\mathrm{5}} }+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *