Question Number 107617 by mathdave last updated on 11/Aug/20
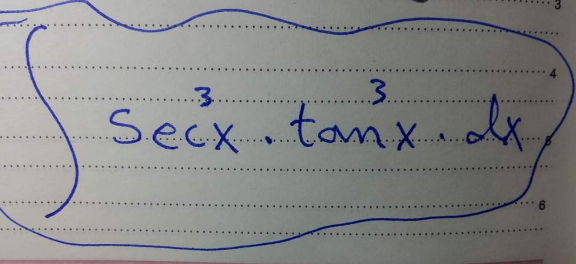
Answered by Ar Brandon last updated on 11/Aug/20
![I=∫sec^3 xtan^3 xdx =∫sec^2 x(sec^2 x−1)secxtanxdx =∫(sec^4 x−sec^2 x)d(secx) =[((sec^5 x)/5)−((sec^3 x)/3)]+C](https://www.tinkutara.com/question/Q107622.png)
$$\mathrm{I}=\int\mathrm{sec}^{\mathrm{3}} \mathrm{xtan}^{\mathrm{3}} \mathrm{xdx} \\ $$$$\:\:=\int\mathrm{sec}^{\mathrm{2}} \mathrm{x}\left(\mathrm{sec}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)\mathrm{secxtanxdx} \\ $$$$\:\:=\int\left(\mathrm{sec}^{\mathrm{4}} \mathrm{x}−\mathrm{sec}^{\mathrm{2}} \mathrm{x}\right)\mathrm{d}\left(\mathrm{secx}\right) \\ $$$$\:\:=\left[\frac{\mathrm{sec}^{\mathrm{5}} \mathrm{x}}{\mathrm{5}}−\frac{\mathrm{sec}^{\mathrm{3}} \mathrm{x}}{\mathrm{3}}\right]+\mathcal{C} \\ $$
