Question Number 107656 by bemath last updated on 12/Aug/20

Answered by john santu last updated on 12/Aug/20
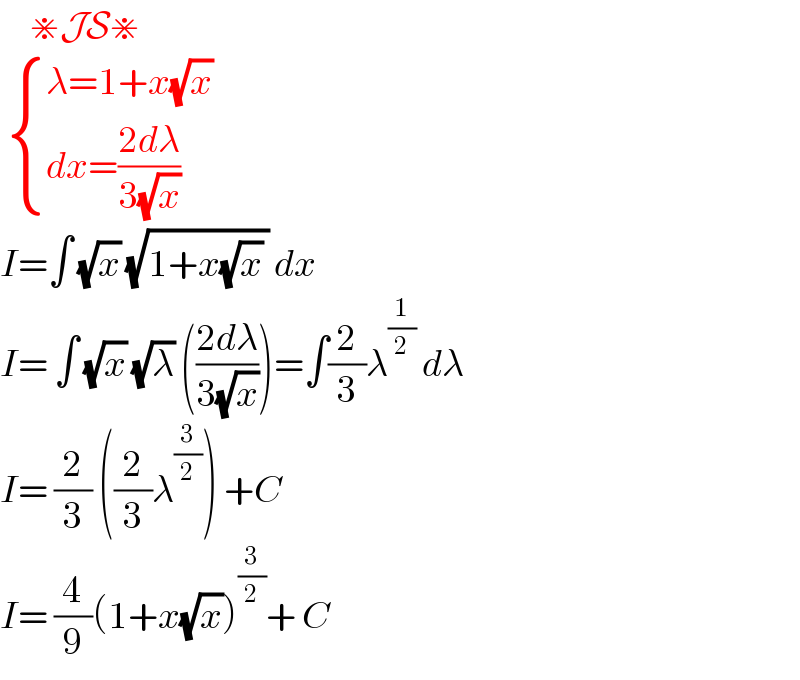
$$\:\:\:\:\:\divideontimes\mathcal{JS}\divideontimes \\ $$$$\:\begin{cases}{\lambda=\mathrm{1}+{x}\sqrt{{x}}}\\{{dx}=\frac{\mathrm{2}{d}\lambda}{\mathrm{3}\sqrt{{x}}}}\end{cases} \\ $$$${I}=\int\:\sqrt{{x}}\:\sqrt{\mathrm{1}+{x}\sqrt{{x}}\:}\:{dx}\: \\ $$$${I}=\:\int\:\sqrt{{x}}\:\sqrt{\lambda}\:\left(\frac{\mathrm{2}{d}\lambda}{\mathrm{3}\sqrt{{x}}}\right)=\int\frac{\mathrm{2}}{\mathrm{3}}\lambda^{\frac{\mathrm{1}}{\mathrm{2}}} \:{d}\lambda \\ $$$${I}=\:\frac{\mathrm{2}}{\mathrm{3}}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\lambda^{\frac{\mathrm{3}}{\mathrm{2}}} \right)\:+{C}\: \\ $$$${I}=\:\frac{\mathrm{4}}{\mathrm{9}}\left(\mathrm{1}+{x}\sqrt{{x}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\:{C}\: \\ $$
Answered by 1549442205PVT last updated on 12/Aug/20
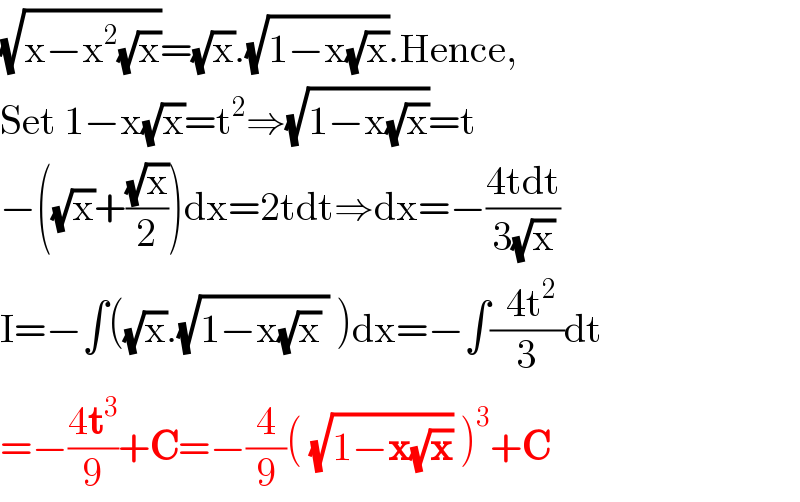
$$\sqrt{\mathrm{x}−\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{x}}}=\sqrt{\mathrm{x}}.\sqrt{\mathrm{1}−\mathrm{x}\sqrt{\mathrm{x}}}.\mathrm{Hence}, \\ $$$$\mathrm{Set}\:\mathrm{1}−\mathrm{x}\sqrt{\mathrm{x}}=\mathrm{t}^{\mathrm{2}} \Rightarrow\sqrt{\mathrm{1}−\mathrm{x}\sqrt{\mathrm{x}}}=\mathrm{t} \\ $$$$−\left(\sqrt{\mathrm{x}}+\frac{\sqrt{\mathrm{x}}}{\mathrm{2}}\right)\mathrm{dx}=\mathrm{2tdt}\Rightarrow\mathrm{dx}=−\frac{\mathrm{4tdt}}{\mathrm{3}\sqrt{\mathrm{x}}} \\ $$$$\mathrm{I}=−\int\left(\sqrt{\mathrm{x}}.\sqrt{\mathrm{1}−\mathrm{x}\sqrt{\mathrm{x}}\:}\:\right)\mathrm{dx}=−\int\frac{\:\:\mathrm{4t}^{\mathrm{2}} \:}{\mathrm{3}}\mathrm{dt} \\ $$$$=−\frac{\mathrm{4}\boldsymbol{\mathrm{t}}^{\mathrm{3}} }{\mathrm{9}}+\boldsymbol{\mathrm{C}}=−\frac{\mathrm{4}}{\mathrm{9}}\left(\:\sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}\sqrt{\boldsymbol{\mathrm{x}}}}\:\right)^{\mathrm{3}} +\boldsymbol{\mathrm{C}} \\ $$
Commented by bemath last updated on 12/Aug/20
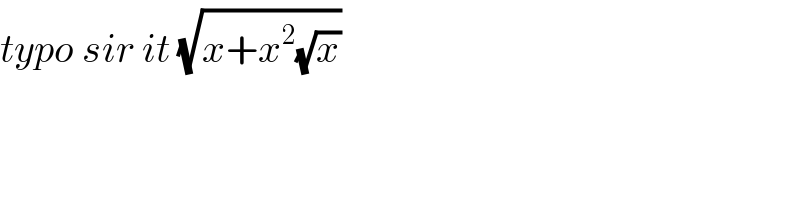
$${typo}\:{sir}\:{it}\:\sqrt{{x}+{x}^{\mathrm{2}} \sqrt{{x}}}\: \\ $$
Answered by Dwaipayan Shikari last updated on 12/Aug/20
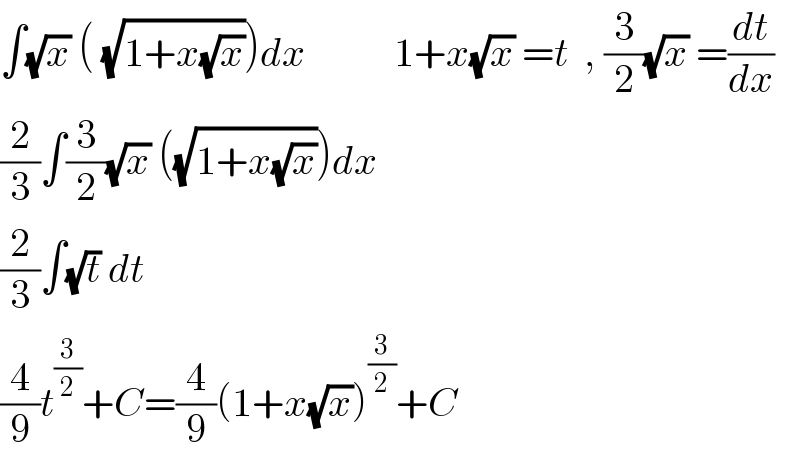
$$\int\sqrt{{x}}\:\left(\:\sqrt{\mathrm{1}+{x}\sqrt{{x}}}\right){dx}\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}+{x}\sqrt{{x}}\:={t}\:\:,\:\frac{\mathrm{3}}{\mathrm{2}}\sqrt{{x}}\:=\frac{{dt}}{{dx}} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{3}}{\mathrm{2}}\sqrt{{x}}\:\left(\sqrt{\mathrm{1}+{x}\sqrt{{x}}}\right){dx} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\int\sqrt{{t}}\:{dt} \\ $$$$\frac{\mathrm{4}}{\mathrm{9}}{t}^{\frac{\mathrm{3}}{\mathrm{2}}} +{C}=\frac{\mathrm{4}}{\mathrm{9}}\left(\mathrm{1}+{x}\sqrt{{x}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +{C} \\ $$
