Question Number 107696 by ajfour last updated on 12/Aug/20
Commented by ajfour last updated on 12/Aug/20
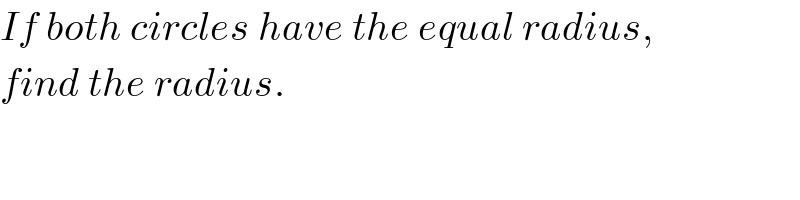
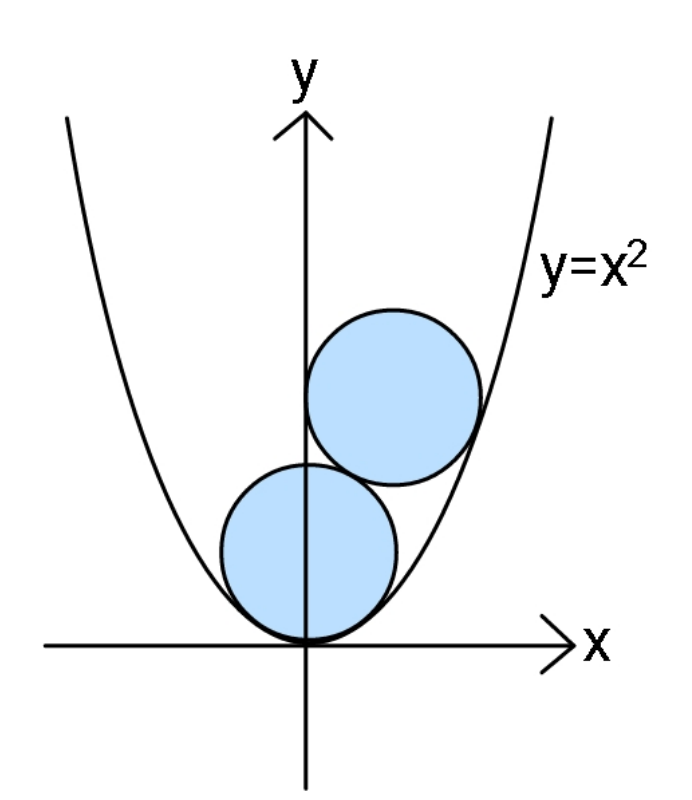
$${If}\:{both}\:{circles}\:{have}\:{the}\:{equal}\:{radius}, \\ $$$${find}\:{the}\:{radius}. \\ $$
Answered by mr W last updated on 20/Aug/20
Commented by mr W last updated on 21/Aug/20
![A(a,a^2 ) tan θ=y′=2a B(b,b^2 ) tan ϕ=y′=2b x_C =a−r sin θ=0 y_C =a^2 +r cos θ ⇒a=((tan θ)/2)=r sin θ ⇒cos θ=(1/(2r)) y_C =((tan^2 θ)/4)+(1/2)=((1−cos^2 θ)/(4 cos^2 θ))+(1/2)=r^2 +(1/4) x_D =b−r sin ϕ=r y_D =b^2 +r cos ϕ b=((tan ϕ)/2)=r(1+sin ϕ) ⇒r=((tan ϕ)/(2(1+sin ϕ))) y_D =r^2 (1+sin^2 ϕ+2 sin ϕ)+r cos ϕ (2r)^2 −r^2 =(y_D −y_C )^2 3r^2 =[r^2 sin ϕ(2+sin ϕ)+r cos ϕ−(1/4)]^2 ⇒((12 tan^2 ϕ)/((1+sin ϕ)^2 ))=[((tan^2 ϕ sin ϕ (2+sin ϕ))/((1+sin ϕ)^2 ))+((2 sin ϕ)/(1+sin ϕ))−1]^2 ⇒ϕ=1.1875=68.039° ⇒r=0.6433](https://www.tinkutara.com/question/Q109060.png)
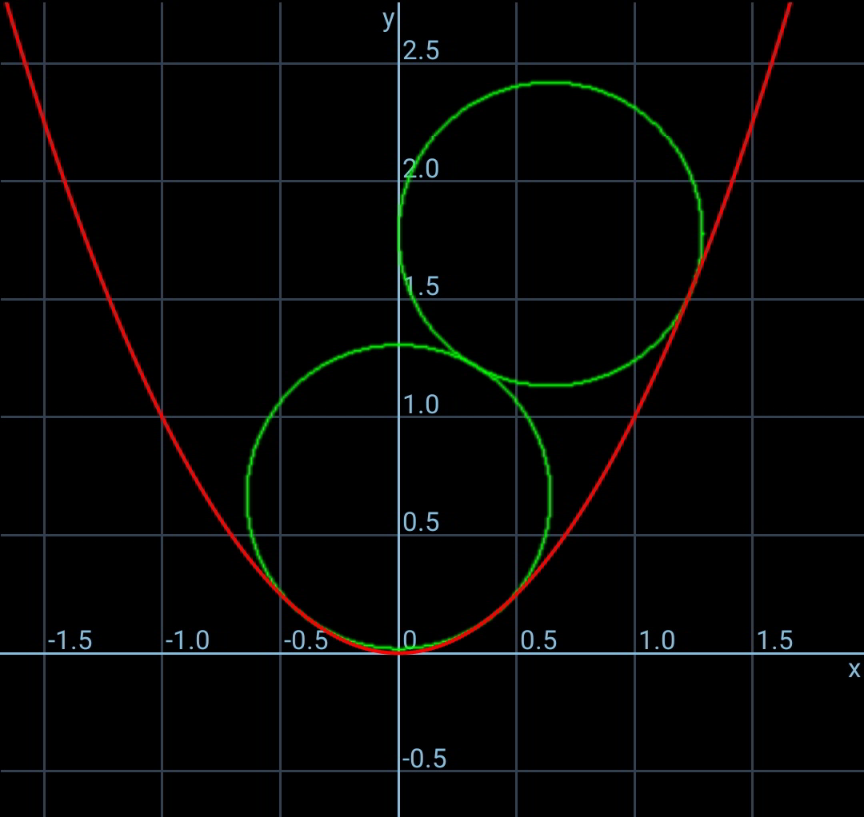
$${A}\left({a},{a}^{\mathrm{2}} \right) \\ $$$$\mathrm{tan}\:\theta={y}'=\mathrm{2}{a} \\ $$$${B}\left({b},{b}^{\mathrm{2}} \right) \\ $$$$\mathrm{tan}\:\varphi={y}'=\mathrm{2}{b} \\ $$$$ \\ $$$${x}_{{C}} ={a}−{r}\:\mathrm{sin}\:\theta=\mathrm{0} \\ $$$${y}_{{C}} ={a}^{\mathrm{2}} +{r}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{a}=\frac{\mathrm{tan}\:\theta}{\mathrm{2}}={r}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\frac{\mathrm{1}}{\mathrm{2}{r}} \\ $$$${y}_{{C}} =\frac{\mathrm{tan}^{\mathrm{2}} \:\theta}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\theta}{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta}+\frac{\mathrm{1}}{\mathrm{2}}={r}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$ \\ $$$${x}_{{D}} ={b}−{r}\:\mathrm{sin}\:\varphi={r} \\ $$$${y}_{{D}} ={b}^{\mathrm{2}} +{r}\:\mathrm{cos}\:\varphi \\ $$$${b}=\frac{\mathrm{tan}\:\varphi}{\mathrm{2}}={r}\left(\mathrm{1}+\mathrm{sin}\:\varphi\right) \\ $$$$\Rightarrow{r}=\frac{\mathrm{tan}\:\varphi}{\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\varphi\right)} \\ $$$${y}_{{D}} ={r}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\varphi+\mathrm{2}\:\mathrm{sin}\:\varphi\right)+{r}\:\mathrm{cos}\:\varphi \\ $$$$\left(\mathrm{2}{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} =\left({y}_{{D}} −{y}_{{C}} \right)^{\mathrm{2}} \\ $$$$\mathrm{3}{r}^{\mathrm{2}} =\left[{r}^{\mathrm{2}} \mathrm{sin}\:\varphi\left(\mathrm{2}+\mathrm{sin}\:\varphi\right)+{r}\:\mathrm{cos}\:\varphi−\frac{\mathrm{1}}{\mathrm{4}}\right]^{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{12}\:\mathrm{tan}^{\mathrm{2}} \:\varphi}{\left(\mathrm{1}+\mathrm{sin}\:\varphi\right)^{\mathrm{2}} }=\left[\frac{\mathrm{tan}^{\mathrm{2}} \:\varphi\:\mathrm{sin}\:\varphi\:\left(\mathrm{2}+\mathrm{sin}\:\varphi\right)}{\left(\mathrm{1}+\mathrm{sin}\:\varphi\right)^{\mathrm{2}} }+\frac{\mathrm{2}\:\mathrm{sin}\:\varphi}{\mathrm{1}+\mathrm{sin}\:\varphi}−\mathrm{1}\right]^{\mathrm{2}} \\ $$$$\Rightarrow\varphi=\mathrm{1}.\mathrm{1875}=\mathrm{68}.\mathrm{039}° \\ $$$$\Rightarrow{r}=\mathrm{0}.\mathrm{6433} \\ $$
Commented by mr W last updated on 20/Aug/20
Commented by ajfour last updated on 21/Aug/20
$${Thank}\:{u}\:{Sir},\:{marvellous}\:{solution}! \\ $$
