Question Number 107718 by mohammad17 last updated on 12/Aug/20

Answered by Aziztisffola last updated on 12/Aug/20

$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\overset{−} {\mathrm{z}}_{\mathrm{n}} =\overline {\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{z}_{\mathrm{n}} }=\:\overset{−} {\mathrm{s}} \\ $$
Commented by mohammad17 last updated on 12/Aug/20
$${sir}\:{i}\:{want}\:{details}\:{the}\:{solution} \\ $$
Commented by Aziztisffola last updated on 12/Aug/20
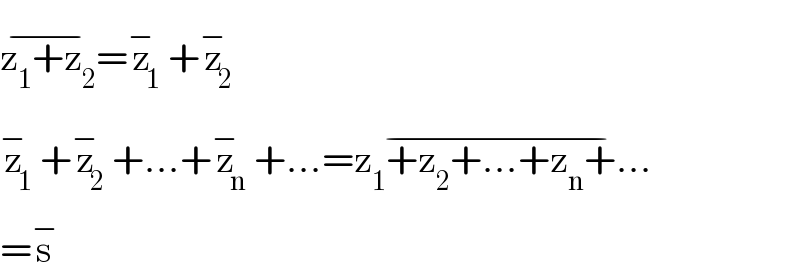
$$\overline {\mathrm{z}_{\mathrm{1}} +\mathrm{z}_{\mathrm{2}} }=\overset{−} {\mathrm{z}}_{\mathrm{1}} +\overset{−} {\mathrm{z}}_{\mathrm{2}} \\ $$$$\overset{−} {\mathrm{z}}_{\mathrm{1}} +\overset{−} {\mathrm{z}}_{\mathrm{2}} +…+\overset{−} {\mathrm{z}}_{\mathrm{n}} +…=\overline {\mathrm{z}_{\mathrm{1}} +\mathrm{z}_{\mathrm{2}} +…+\mathrm{z}_{\mathrm{n}} +…} \\ $$$$=\overset{−} {\mathrm{s}} \\ $$
Commented by mohammad17 last updated on 12/Aug/20

$${thank}\:{you}\:{sir} \\ $$
Commented by Aziztisffola last updated on 12/Aug/20

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$
