Question Number 107766 by mohammad17 last updated on 12/Aug/20

Answered by bobhans last updated on 12/Aug/20
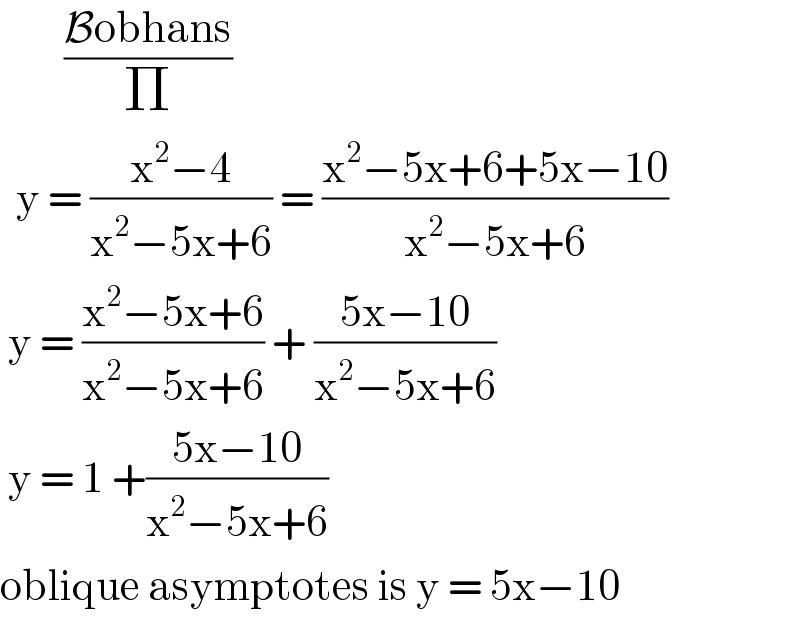
$$\:\:\:\:\:\:\:\:\frac{\mathcal{B}\mathrm{obhans}}{\Pi} \\ $$$$\:\:\mathrm{y}\:=\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{4}}{\mathrm{x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{6}}\:=\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{6}+\mathrm{5x}−\mathrm{10}}{\mathrm{x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{6}} \\ $$$$\:\mathrm{y}\:=\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{6}}{\mathrm{x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{6}}\:+\:\frac{\mathrm{5x}−\mathrm{10}}{\mathrm{x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{6}}\: \\ $$$$\:\mathrm{y}\:=\:\mathrm{1}\:+\frac{\mathrm{5x}−\mathrm{10}}{\mathrm{x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{6}} \\ $$$$\mathrm{oblique}\:\mathrm{asymptotes}\:\mathrm{is}\:\mathrm{y}\:=\:\mathrm{5x}−\mathrm{10} \\ $$
Commented by mohammad17 last updated on 12/Aug/20

$${thank}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 12/Aug/20

$$\mathrm{no}\:\mathrm{correct}\:\mathrm{sir}\:. \\ $$
Answered by ajfour last updated on 12/Aug/20
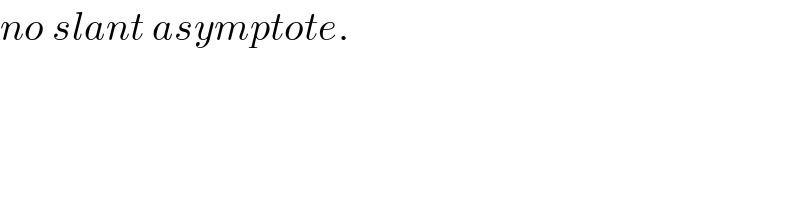
$${no}\:{slant}\:{asymptote}. \\ $$
Answered by mathmax by abdo last updated on 12/Aug/20
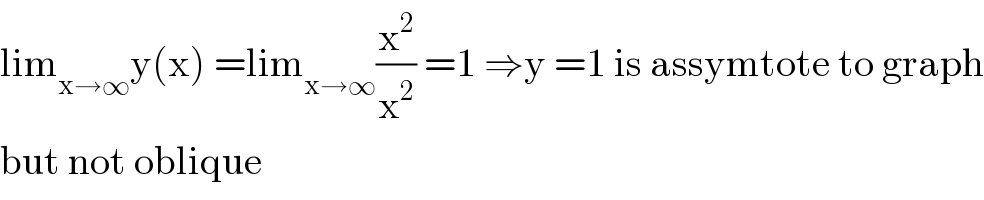
$$\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\:=\mathrm{1}\:\Rightarrow\mathrm{y}\:=\mathrm{1}\:\mathrm{is}\:\mathrm{assymtote}\:\mathrm{to}\:\mathrm{graph} \\ $$$$\mathrm{but}\:\mathrm{not}\:\mathrm{oblique}\:\: \\ $$
Answered by mathmax by abdo last updated on 12/Aug/20
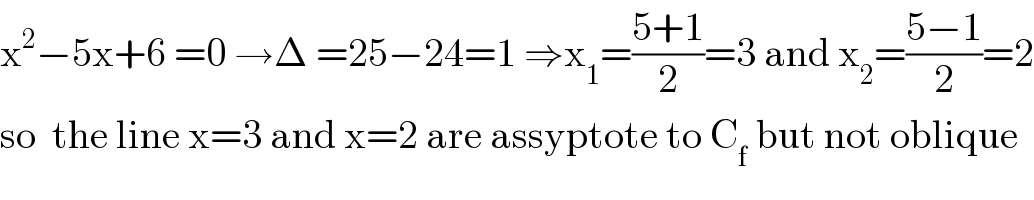
$$\mathrm{x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{6}\:=\mathrm{0}\:\rightarrow\Delta\:=\mathrm{25}−\mathrm{24}=\mathrm{1}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =\frac{\mathrm{5}+\mathrm{1}}{\mathrm{2}}=\mathrm{3}\:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} =\frac{\mathrm{5}−\mathrm{1}}{\mathrm{2}}=\mathrm{2} \\ $$$$\mathrm{so}\:\:\mathrm{the}\:\mathrm{line}\:\mathrm{x}=\mathrm{3}\:\mathrm{and}\:\mathrm{x}=\mathrm{2}\:\mathrm{are}\:\mathrm{assyptote}\:\mathrm{to}\:\mathrm{C}_{\mathrm{f}} \:\mathrm{but}\:\mathrm{not}\:\mathrm{oblique} \\ $$
