Question Number 108017 by mathdave last updated on 13/Aug/20
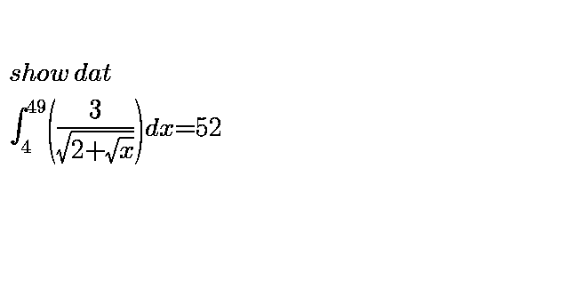
Answered by hgrocks last updated on 13/Aug/20
![2 + (√x) = y^2 ⇒ (√x) = y^2 − 2 (1/(2(√x))).(1/(2(√(2+(√x))))) dx = dy (1/( (√(2+(√x))))) dx = 4(y^2 −2) I = 12∫_2 ^3 (y^2 − 2)dy I = 12[(y^3 /3) − 2y]_2 ^3 I = 12[((19)/3) − 2] = 76 − 24 I = 52 ★HG★](https://www.tinkutara.com/question/Q108021.png)
$$\mathrm{2}\:+\:\sqrt{\mathrm{x}}\:=\:\mathrm{y}^{\mathrm{2}} \Rightarrow\:\sqrt{\mathrm{x}}\:=\:\mathrm{y}^{\mathrm{2}} \:−\:\mathrm{2} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}}.\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}+\sqrt{\mathrm{x}}}}\:\mathrm{dx}\:=\:\mathrm{dy} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}+\sqrt{\mathrm{x}}}}\:\mathrm{dx}\:=\:\mathrm{4}\left(\mathrm{y}^{\mathrm{2}} −\mathrm{2}\right) \\ $$$$ \\ $$$$\mathrm{I}\:=\:\mathrm{12}\underset{\mathrm{2}} {\overset{\mathrm{3}} {\int}}\left(\mathrm{y}^{\mathrm{2}} \:−\:\mathrm{2}\right)\mathrm{dy} \\ $$$$\mathrm{I}\:=\:\mathrm{12}\left[\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}\:−\:\mathrm{2y}\right]_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$\mathrm{I}\:=\:\mathrm{12}\left[\frac{\mathrm{19}}{\mathrm{3}}\:−\:\mathrm{2}\right] \\ $$$$\:\:=\:\mathrm{76}\:−\:\mathrm{24} \\ $$$$\mathrm{I}\:=\:\mathrm{52} \\ $$$$ \\ $$$$\bigstar\boldsymbol{\mathrm{HG}}\bigstar \\ $$
Answered by mathmax by abdo last updated on 13/Aug/20
![I =∫_4 ^(49) (3/( (√(2+(√x)))))dx we do the changement (√(2+(√x)))=t ⇒2+(√x)=t^2 ⇒ (√x)=t^2 −2 ⇒x =(t^2 −2)^2 ⇒I =3∫_2 ^3 ((2(2t)(t^2 −2))/t) dt =12 ∫_2 ^3 (t^2 −2)dt =12 [(t^3 /3)−2t]_2 ^3 =12{9−6−(8/3)+4} =12{7−(8/3)} =(12.7)−32 =84−32 =52](https://www.tinkutara.com/question/Q108025.png)
$$\mathrm{I}\:=\int_{\mathrm{4}} ^{\mathrm{49}} \:\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}+\sqrt{\mathrm{x}}}}\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\sqrt{\mathrm{2}+\sqrt{\mathrm{x}}}=\mathrm{t}\:\Rightarrow\mathrm{2}+\sqrt{\mathrm{x}}=\mathrm{t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\sqrt{\mathrm{x}}=\mathrm{t}^{\mathrm{2}} −\mathrm{2}\:\Rightarrow\mathrm{x}\:=\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} \:\Rightarrow\mathrm{I}\:=\mathrm{3}\int_{\mathrm{2}} ^{\mathrm{3}} \:\:\:\frac{\mathrm{2}\left(\mathrm{2t}\right)\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2}\right)}{\mathrm{t}}\:\mathrm{dt} \\ $$$$=\mathrm{12}\:\int_{\mathrm{2}} ^{\mathrm{3}} \:\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2}\right)\mathrm{dt}\:=\mathrm{12}\:\left[\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{2t}\right]_{\mathrm{2}} ^{\mathrm{3}} \:=\mathrm{12}\left\{\mathrm{9}−\mathrm{6}−\frac{\mathrm{8}}{\mathrm{3}}+\mathrm{4}\right\} \\ $$$$=\mathrm{12}\left\{\mathrm{7}−\frac{\mathrm{8}}{\mathrm{3}}\right\}\:=\left(\mathrm{12}.\mathrm{7}\right)−\mathrm{32}\:=\mathrm{84}−\mathrm{32}\:=\mathrm{52} \\ $$
