Question Number 108034 by mathdave last updated on 14/Aug/20
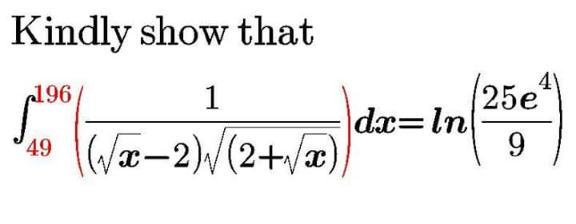
Answered by mathmax by abdo last updated on 14/Aug/20
![I =∫_(49) ^(196) (dx/(((√x)−2)(√(2+(√x))))) we do tbe cha7gement (√x)=t ⇒ I =∫_7 ^(14) ((2t dt)/((t−2)(√(2+t)))) dt =2 ∫_7 ^(14) ((tdt)/((t−2)(√(2+t)))) =_((√(2+t))=u) 2∫_3 ^4 ((u^2 −2)/((u^2 −4)u)) (2u)du =4 ∫_3 ^4 ((u^2 −2)/(u^2 −4))du =4 ∫_3 ^4 ((u^2 −4+2)/(u^2 −4))du =4 ∫_3 ^4 du +8 ∫_3 ^4 (du/((u−2)(u+2))) =4 +2∫_3 ^4 ((1/(u−2))−(1/(u+2)))du =4 +2 [ln∣((u−2)/(u+2))∣]_3 ^4 =4 +2{ln((2/6))−ln((1/5))} =4+2{−ln(3)+ln)5)} =4 +2ln((5/3)) =ln(e^4 )+ln(((25)/9)) =ln(((25)/9)e^4 )](https://www.tinkutara.com/question/Q108035.png)
$$\mathrm{I}\:=\int_{\mathrm{49}} ^{\mathrm{196}} \:\:\:\frac{\mathrm{dx}}{\left(\sqrt{\mathrm{x}}−\mathrm{2}\right)\sqrt{\mathrm{2}+\sqrt{\mathrm{x}}}}\:\mathrm{we}\:\mathrm{do}\:\mathrm{tbe}\:\mathrm{cha7gement}\:\:\sqrt{\mathrm{x}}=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{7}} ^{\mathrm{14}} \:\frac{\mathrm{2t}\:\mathrm{dt}}{\left(\mathrm{t}−\mathrm{2}\right)\sqrt{\mathrm{2}+\mathrm{t}}}\:\mathrm{dt}\:=\mathrm{2}\:\int_{\mathrm{7}} ^{\mathrm{14}} \:\frac{\mathrm{tdt}}{\left(\mathrm{t}−\mathrm{2}\right)\sqrt{\mathrm{2}+\mathrm{t}}} \\ $$$$=_{\sqrt{\mathrm{2}+\mathrm{t}}=\mathrm{u}} \:\:\mathrm{2}\int_{\mathrm{3}} ^{\mathrm{4}} \:\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{2}}{\left(\mathrm{u}^{\mathrm{2}} −\mathrm{4}\right)\mathrm{u}}\:\left(\mathrm{2u}\right)\mathrm{du}\:=\mathrm{4}\:\int_{\mathrm{3}} ^{\mathrm{4}} \:\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{2}}{\mathrm{u}^{\mathrm{2}} −\mathrm{4}}\mathrm{du} \\ $$$$=\mathrm{4}\:\int_{\mathrm{3}} ^{\mathrm{4}} \:\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{4}+\mathrm{2}}{\mathrm{u}^{\mathrm{2}} −\mathrm{4}}\mathrm{du}\:=\mathrm{4}\:\int_{\mathrm{3}} ^{\mathrm{4}} \:\mathrm{du}\:+\mathrm{8}\:\int_{\mathrm{3}} ^{\mathrm{4}} \:\frac{\mathrm{du}}{\left(\mathrm{u}−\mathrm{2}\right)\left(\mathrm{u}+\mathrm{2}\right)} \\ $$$$=\mathrm{4}\:+\mathrm{2}\int_{\mathrm{3}} ^{\mathrm{4}} \left(\frac{\mathrm{1}}{\mathrm{u}−\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{u}+\mathrm{2}}\right)\mathrm{du} \\ $$$$=\mathrm{4}\:+\mathrm{2}\:\left[\mathrm{ln}\mid\frac{\mathrm{u}−\mathrm{2}}{\mathrm{u}+\mathrm{2}}\mid\right]_{\mathrm{3}} ^{\mathrm{4}} \:=\mathrm{4}\:+\mathrm{2}\left\{\mathrm{ln}\left(\frac{\mathrm{2}}{\mathrm{6}}\right)−\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{5}}\right)\right\} \\ $$$$\left.=\left.\mathrm{4}+\mathrm{2}\left\{−\mathrm{ln}\left(\mathrm{3}\right)+\mathrm{ln}\right)\mathrm{5}\right)\right\}\:=\mathrm{4}\:+\mathrm{2ln}\left(\frac{\mathrm{5}}{\mathrm{3}}\right)\:=\mathrm{ln}\left(\mathrm{e}^{\mathrm{4}} \right)+\mathrm{ln}\left(\frac{\mathrm{25}}{\mathrm{9}}\right) \\ $$$$=\mathrm{ln}\left(\frac{\mathrm{25}}{\mathrm{9}}\mathrm{e}^{\mathrm{4}} \right) \\ $$
