Menu Close

Question-108067

Tinku Tara 0 Comments
Pin




Question Number 108067 by I want to learn more last updated on 14/Aug/20
Answered by 1549442205PVT last updated on 14/Aug/20
Commented by 1549442205PVT last updated on 14/Aug/20
BD=2a,CD=3a,CE=12,AE=6,AF=3 BF=x? First we prove following Xeva′s therem “Given the triangle ABC and D,E,F are three points lying on the sides BC AC and AB respectively.Then three lines AD,BE and CF are concurren at a point G if and only if ((BD)/(DC)).((CE)/(EA)).((AF)/(FB))=1(∗)” i)Let AD,BE,CF are omcurrent at G we need to prove the equality (∗) Indeed,we have ((BD)/(DC))=(S_(ABD) /S_(ACD) )=(S_(GBD) /S_(GCD) )= =((S_(ABD) −S_(GBD) )/(S_(ACD) −S_(GCD) ))=(S_(AGB) /S_(AGC) )(1).Similarly,we have also ((CE)/(EA))=(S_(BGC) /S_(BGA) ) (2),((AF)/(FB))=(S_(AGC) /S_(BGC) )(3) Multiplying three above equalities together we obtain ((BD)/(DC)).((CE)/(EA)).((AF)/(FB))=(S_(AGB) /S_(AGC) )×(S_(BGC) /S_(BGA) ) ×(S_(AGC) /S_(BGC) )=1(q.e.d) Now suppose had the equality (∗) we prove AD,BE,CF are concurrent.Indeed, denote by G the intersection point of BE and CF.Let the ray AG meet BC at the point D′.Then by above result we get ((BD′)/(D′C)).((CE)/(.EA)).((AF)/(FB))=1.Then combining to (∗) we get ((BD′)/(D′C))=((BD)/(DC))⇔((BD′)/(BC))=((BD)/(BC)) ⇒D′≡D⇒AD which shows that AD, BE and CF are concurrent at G(q.e.d) Now applying Xeva′s theorem on the given problem we get ((BD)/(DC)).((CE)/(EA)).((AF)/(FB))=1⇔((2a)/(3a)).((12)/6).(3/x)=1⇒((72a)/(18ax))=1 ⇒x=4
$$\mathrm{BD}=\mathrm{2a},\mathrm{CD}=\mathrm{3a},\mathrm{CE}=\mathrm{12},\mathrm{AE}=\mathrm{6},\mathrm{AF}=\mathrm{3} \\ $$$$\mathrm{BF}=\mathrm{x}? \\ $$$$\mathrm{First}\:\mathrm{we}\:\:\mathrm{prove}\:\mathrm{following}\:\mathrm{Xeva}'\mathrm{s}\:\mathrm{therem} \\ $$$$“\mathrm{Given}\:\mathrm{the}\:\mathrm{triangle}\:\mathrm{ABC}\:\mathrm{and}\:\mathrm{D},\mathrm{E},\mathrm{F} \\ $$$$\mathrm{are}\:\mathrm{three}\:\mathrm{points}\:\mathrm{lying}\:\mathrm{on}\:\mathrm{the}\:\mathrm{sides}\:\mathrm{BC} \\ $$$$\mathrm{AC}\:\mathrm{and}\:\mathrm{AB}\:\mathrm{respectively}.\mathrm{Then}\:\mathrm{three} \\ $$$$\mathrm{lines}\:\mathrm{AD},\mathrm{BE}\:\mathrm{and}\:\mathrm{CF}\:\mathrm{are}\:\mathrm{concurren}\:\mathrm{at} \\ $$$$\mathrm{a}\:\mathrm{point}\:\mathrm{G}\:\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if}\:\frac{\mathrm{BD}}{\mathrm{DC}}.\frac{\mathrm{CE}}{\mathrm{EA}}.\frac{\mathrm{AF}}{\mathrm{FB}}=\mathrm{1}\left(\ast\right)'' \\ $$$$\left.\mathrm{i}\right)\mathrm{Let}\:\mathrm{AD},\mathrm{BE},\mathrm{CF}\:\mathrm{are}\:\mathrm{omcurrent}\:\mathrm{at}\:\mathrm{G} \\ $$$$\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{the}\:\mathrm{equality}\:\left(\ast\right) \\ $$$$\mathrm{Indeed},\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{BD}}{\mathrm{DC}}=\frac{\mathrm{S}_{\mathrm{ABD}} }{\mathrm{S}_{\mathrm{ACD}} }=\frac{\mathrm{S}_{\mathrm{GBD}} }{\mathrm{S}_{\mathrm{GCD}} }= \\ $$$$=\frac{\mathrm{S}_{\mathrm{ABD}} −\mathrm{S}_{\mathrm{GBD}} }{\mathrm{S}_{\mathrm{ACD}} −\mathrm{S}_{\mathrm{GCD}} }=\frac{\mathrm{S}_{\mathrm{AGB}} }{\mathrm{S}_{\mathrm{AGC}} }\left(\mathrm{1}\right).\mathrm{Similarly},\mathrm{we} \\ $$$$\mathrm{have}\:\mathrm{also}\:\frac{\mathrm{CE}}{\mathrm{EA}}=\frac{\mathrm{S}_{\mathrm{BGC}} }{\mathrm{S}_{\mathrm{BGA}} }\:\left(\mathrm{2}\right),\frac{\mathrm{AF}}{\mathrm{FB}}=\frac{\mathrm{S}_{\mathrm{AGC}} }{\mathrm{S}_{\mathrm{BGC}} }\left(\mathrm{3}\right) \\ $$$$\mathrm{Multiplying}\:\mathrm{three}\:\mathrm{above}\:\mathrm{equalities}\: \\ $$$$\mathrm{together}\:\mathrm{we}\:\mathrm{obtain} \\ $$$$\frac{\mathrm{BD}}{\mathrm{DC}}.\frac{\mathrm{CE}}{\mathrm{EA}}.\frac{\mathrm{AF}}{\mathrm{FB}}=\frac{\mathrm{S}_{\mathrm{AGB}} }{\mathrm{S}_{\mathrm{AGC}} }×\frac{\mathrm{S}_{\mathrm{BGC}} }{\mathrm{S}_{\mathrm{BGA}} }\:×\frac{\mathrm{S}_{\mathrm{AGC}} }{\mathrm{S}_{\mathrm{BGC}} }=\mathrm{1}\left(\mathrm{q}.\mathrm{e}.\mathrm{d}\right) \\ $$$$\mathrm{Now}\:\mathrm{suppose}\:\mathrm{had}\:\mathrm{the}\:\mathrm{equality}\:\left(\ast\right)\:\mathrm{we} \\ $$$$\mathrm{prove}\:\mathrm{AD},\mathrm{BE},\mathrm{CF}\:\mathrm{are}\:\mathrm{concurrent}.\mathrm{Indeed}, \\ $$$$\mathrm{denote}\:\mathrm{by}\:\mathrm{G}\:\mathrm{the}\:\mathrm{intersection}\:\mathrm{point} \\ $$$$\mathrm{of}\:\mathrm{BE}\:\mathrm{and}\:\mathrm{CF}.\mathrm{Let}\:\mathrm{the}\:\mathrm{ray}\:\mathrm{AG}\:\mathrm{meet}\:\mathrm{BC} \\ $$$$\mathrm{at}\:\mathrm{the}\:\mathrm{point}\:\mathrm{D}'.\mathrm{Then}\:\mathrm{by}\:\mathrm{above}\:\mathrm{result} \\ $$$$\mathrm{we}\:\mathrm{get}\:\frac{\mathrm{BD}'}{\mathrm{D}'\mathrm{C}}.\frac{\mathrm{CE}}{.\mathrm{EA}}.\frac{\mathrm{AF}}{\mathrm{FB}}=\mathrm{1}.\mathrm{Then}\:\mathrm{combining} \\ $$$$\mathrm{to}\:\left(\ast\right)\:\mathrm{we}\:\mathrm{get}\:\frac{\mathrm{BD}'}{\mathrm{D}'\mathrm{C}}=\frac{\mathrm{BD}}{\mathrm{DC}}\Leftrightarrow\frac{\mathrm{BD}'}{\mathrm{BC}}=\frac{\mathrm{BD}}{\mathrm{BC}} \\ $$$$\Rightarrow\mathrm{D}'\equiv\mathrm{D}\Rightarrow\mathrm{AD}\:\:\mathrm{which}\:\mathrm{shows}\:\mathrm{that}\:\mathrm{AD}, \\ $$$$\mathrm{BE}\:\mathrm{and}\:\mathrm{CF}\:\mathrm{are}\:\mathrm{concurrent}\:\mathrm{at}\:\mathrm{G}\left(\mathrm{q}.\mathrm{e}.\mathrm{d}\right) \\ $$$$\mathrm{Now}\:\:\mathrm{applying}\:\mathrm{Xeva}'\mathrm{s}\:\mathrm{theorem}\:\mathrm{on}\:\mathrm{the} \\ $$$$\mathrm{given}\:\mathrm{problem}\:\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{BD}}{\mathrm{DC}}.\frac{\mathrm{CE}}{\mathrm{EA}}.\frac{\mathrm{AF}}{\mathrm{FB}}=\mathrm{1}\Leftrightarrow\frac{\mathrm{2a}}{\mathrm{3a}}.\frac{\mathrm{12}}{\mathrm{6}}.\frac{\mathrm{3}}{\mathrm{x}}=\mathrm{1}\Rightarrow\frac{\mathrm{72a}}{\mathrm{18ax}}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{4} \\ $$
Commented by I want to learn more last updated on 14/Aug/20
I really appreciate sir
$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir} \\ $$
Answered by floor(10²Eta[1]) last updated on 14/Aug/20
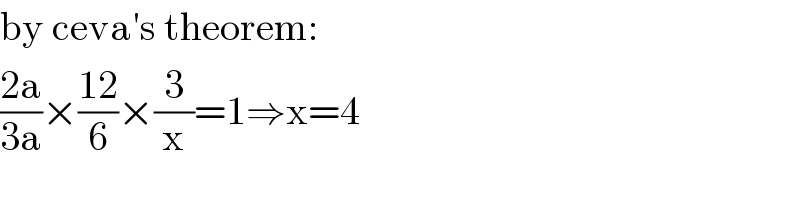
by ceva′s theorem: ((2a)/(3a))×((12)/6)×(3/x)=1⇒x=4
$$\mathrm{by}\:\mathrm{ceva}'\mathrm{s}\:\mathrm{theorem}: \\ $$$$\frac{\mathrm{2a}}{\mathrm{3a}}×\frac{\mathrm{12}}{\mathrm{6}}×\frac{\mathrm{3}}{\mathrm{x}}=\mathrm{1}\Rightarrow\mathrm{x}=\mathrm{4} \\ $$
Commented by I want to learn more last updated on 14/Aug/20
I really appreciate sir
$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *