Question Number 108071 by mathdave last updated on 14/Aug/20
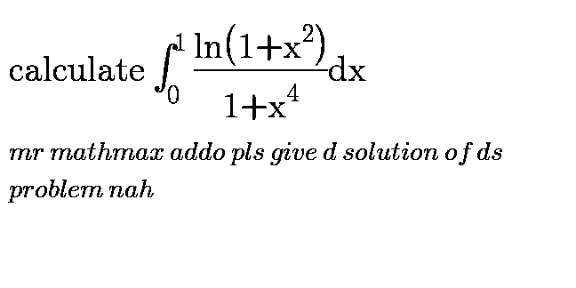
Answered by mathmax by abdo last updated on 14/Aug/20
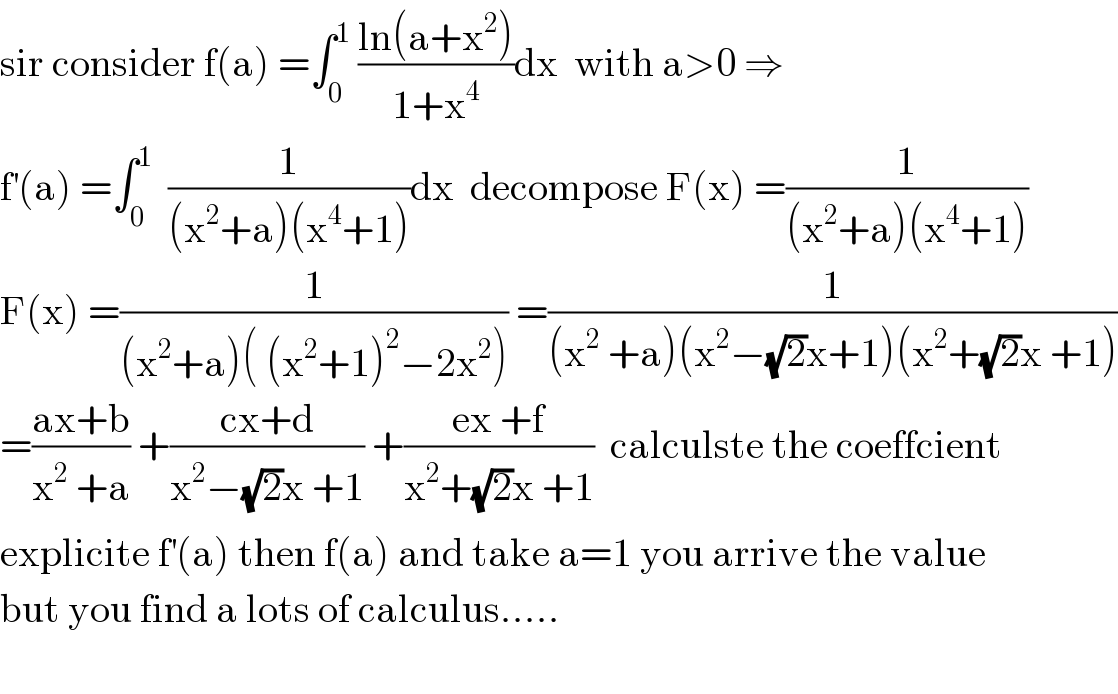
$$\mathrm{sir}\:\mathrm{consider}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{a}+\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}\:\:\mathrm{with}\:\mathrm{a}>\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{a}\right)\left(\mathrm{x}^{\mathrm{4}} +\mathrm{1}\right)}\mathrm{dx}\:\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{a}\right)\left(\mathrm{x}^{\mathrm{4}} +\mathrm{1}\right)} \\ $$$$\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{a}\right)\left(\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2x}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}\right)\left(\mathrm{x}^{\mathrm{2}} −\sqrt{\mathrm{2}}\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\sqrt{\mathrm{2}}\mathrm{x}\:+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{ax}+\mathrm{b}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}}\:+\frac{\mathrm{cx}+\mathrm{d}}{\mathrm{x}^{\mathrm{2}} −\sqrt{\mathrm{2}}\mathrm{x}\:+\mathrm{1}}\:+\frac{\mathrm{ex}\:+\mathrm{f}}{\mathrm{x}^{\mathrm{2}} +\sqrt{\mathrm{2}}\mathrm{x}\:+\mathrm{1}}\:\:\mathrm{calculste}\:\mathrm{the}\:\mathrm{coeffcient} \\ $$$$\mathrm{explicite}\:\mathrm{f}^{'} \left(\mathrm{a}\right)\:\mathrm{then}\:\mathrm{f}\left(\mathrm{a}\right)\:\mathrm{and}\:\mathrm{take}\:\mathrm{a}=\mathrm{1}\:\mathrm{you}\:\mathrm{arrive}\:\mathrm{the}\:\mathrm{value} \\ $$$$\mathrm{but}\:\mathrm{you}\:\mathrm{find}\:\mathrm{a}\:\mathrm{lots}\:\mathrm{of}\:\mathrm{calculus}….. \\ $$$$ \\ $$
