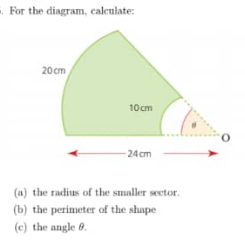
Question Number 108107 by otchereabdullai@gmail.com last updated on 14/Aug/20
Commented by rexfordattacudjoe last updated on 16/Aug/20

$${By}\:{similarities},\frac{{r}}{\mathrm{24}}=\frac{\mathrm{10}}{\mathrm{20}} \\ $$$${r}=\frac{\mathrm{10}×\mathrm{24}}{\mathrm{20}} \\ $$$${r}=\mathrm{12}{cm} \\ $$
Commented by rexfordattacudjoe last updated on 16/Aug/20

$${length}\:{of}\:{an}\:{arc}=\frac{\theta}{\mathrm{360}}×\mathrm{2}\Pi{r} \\ $$$$\mathrm{20}=\frac{\theta}{\mathrm{360}}×\mathrm{2}\left(\frac{\mathrm{22}}{\mathrm{7}}\right)\left(\mathrm{24}\right) \\ $$$$\mathrm{50400}=\mathrm{1056}\theta \\ $$$$\theta=\mathrm{47}.\mathrm{7}° \\ $$
Answered by JDamian last updated on 14/Aug/20
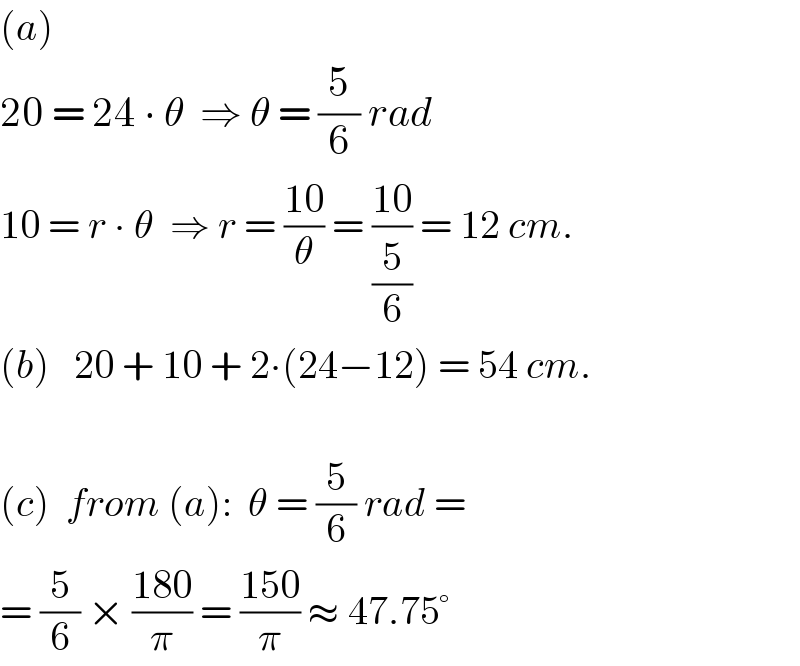
$$\left({a}\right) \\ $$$$\mathrm{20}\:=\:\mathrm{24}\:\centerdot\:\theta\:\:\Rightarrow\:\theta\:=\:\frac{\mathrm{5}}{\mathrm{6}}\:{rad} \\ $$$$\mathrm{10}\:=\:{r}\:\centerdot\:\theta\:\:\Rightarrow\:{r}\:=\:\frac{\mathrm{10}}{\theta}\:=\:\frac{\mathrm{10}}{\frac{\mathrm{5}}{\mathrm{6}}}\:=\:\mathrm{12}\:{cm}. \\ $$$$\left({b}\right)\:\:\:\mathrm{20}\:+\:\mathrm{10}\:+\:\mathrm{2}\centerdot\left(\mathrm{24}−\mathrm{12}\right)\:=\:\mathrm{54}\:{cm}. \\ $$$$ \\ $$$$\left({c}\right)\:\:{from}\:\left({a}\right):\:\:\theta\:=\:\frac{\mathrm{5}}{\mathrm{6}}\:{rad}\:= \\ $$$$=\:\frac{\mathrm{5}}{\mathrm{6}}\:×\:\frac{\mathrm{180}}{\pi}\:=\:\frac{\mathrm{150}}{\pi}\:\approx\:\mathrm{47}.\mathrm{75}° \\ $$
Commented by otchereabdullai@gmail.com last updated on 15/Aug/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
