Question Number 108131 by mathdave last updated on 14/Aug/20
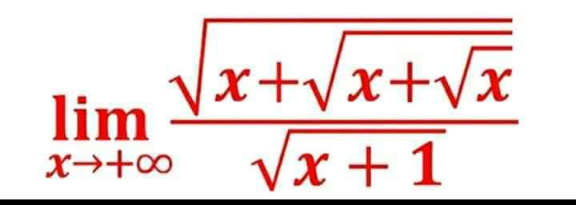
Commented by Her_Majesty last updated on 14/Aug/20
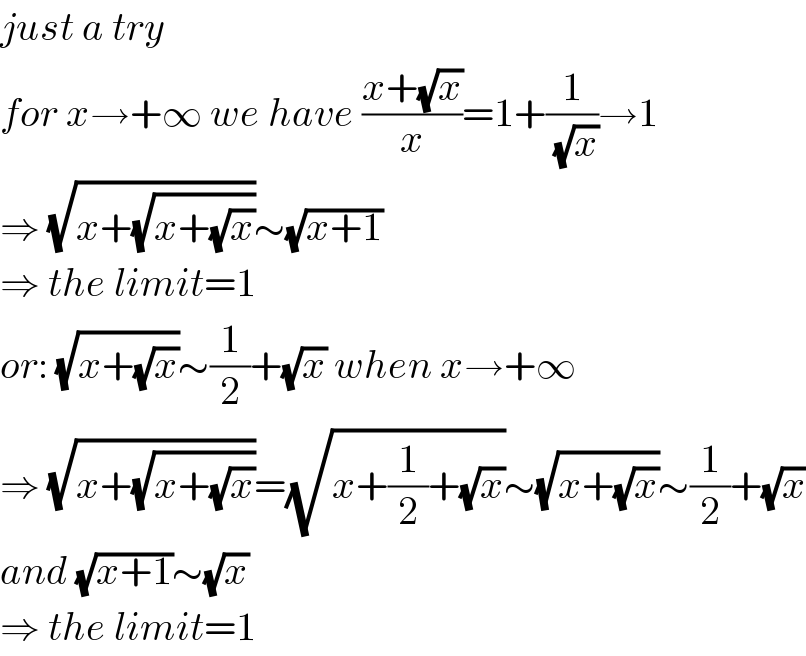
$${just}\:{a}\:{try} \\ $$$${for}\:{x}\rightarrow+\infty\:{we}\:{have}\:\frac{{x}+\sqrt{{x}}}{{x}}=\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{{x}}}\rightarrow\mathrm{1} \\ $$$$\Rightarrow\:\sqrt{{x}+\sqrt{{x}+\sqrt{{x}}}}\sim\sqrt{{x}+\mathrm{1}} \\ $$$$\Rightarrow\:{the}\:{limit}=\mathrm{1} \\ $$$${or}:\:\sqrt{{x}+\sqrt{{x}}}\sim\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{{x}}\:{when}\:{x}\rightarrow+\infty \\ $$$$\Rightarrow\:\sqrt{{x}+\sqrt{{x}+\sqrt{{x}}}}=\sqrt{{x}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{{x}}}\sim\sqrt{{x}+\sqrt{{x}}}\sim\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{{x}} \\ $$$${and}\:\sqrt{{x}+\mathrm{1}}\sim\sqrt{{x}} \\ $$$$\Rightarrow\:{the}\:{limit}=\mathrm{1} \\ $$
Answered by abdomathmax last updated on 14/Aug/20
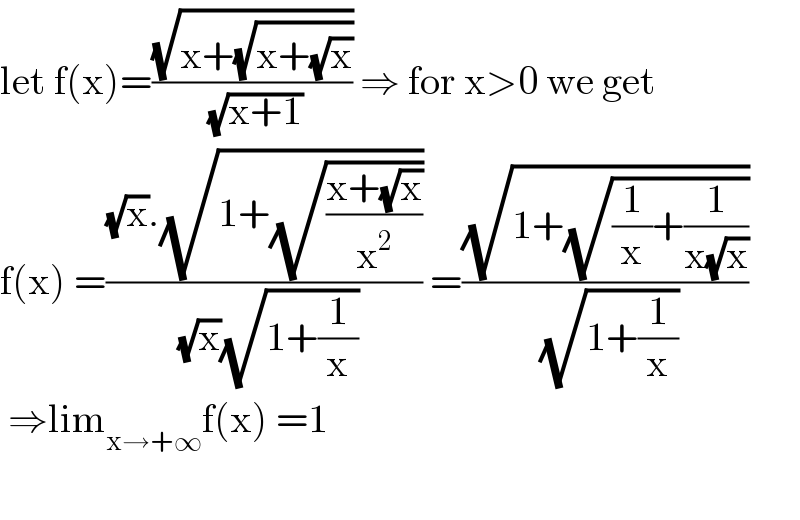
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}}}{\:\sqrt{\mathrm{x}+\mathrm{1}}}\:\Rightarrow\:\mathrm{for}\:\mathrm{x}>\mathrm{0}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\sqrt{\mathrm{x}}.\sqrt{\mathrm{1}+\sqrt{\frac{\mathrm{x}+\sqrt{\mathrm{x}}}{\mathrm{x}^{\mathrm{2}} }}}}{\:\sqrt{\mathrm{x}}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}}}\:=\frac{\sqrt{\mathrm{1}+\sqrt{\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}\sqrt{\mathrm{x}}}}}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}}} \\ $$$$\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{1} \\ $$$$ \\ $$
Commented by Her_Majesty last updated on 14/Aug/20

$${great}! \\ $$
Commented by abdomathmax last updated on 15/Aug/20

$$\mathrm{thanks} \\ $$
Answered by bemath last updated on 15/Aug/20
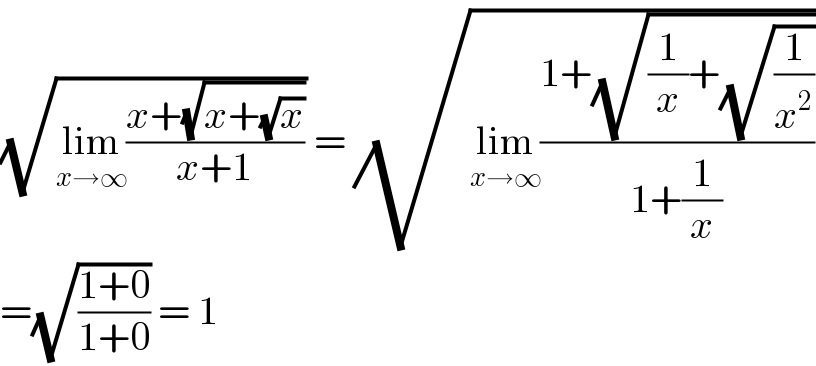
$$\sqrt{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{x}+\sqrt{{x}+\sqrt{{x}}}}{{x}+\mathrm{1}}}\:=\:\sqrt{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}+\sqrt{\frac{\mathrm{1}}{{x}}+\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}}}{\mathrm{1}+\frac{\mathrm{1}}{{x}}}} \\ $$$$=\sqrt{\frac{\mathrm{1}+\mathrm{0}}{\mathrm{1}+\mathrm{0}}}\:=\:\mathrm{1} \\ $$
Answered by 1549442205PVT last updated on 15/Aug/20
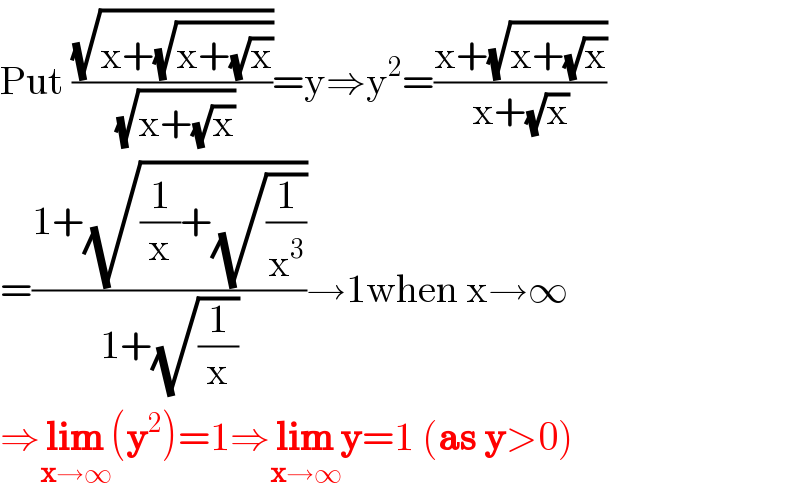
$$\mathrm{Put}\:\frac{\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}}}{\:\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}}=\mathrm{y}\Rightarrow\mathrm{y}^{\mathrm{2}} =\frac{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}}{\mathrm{x}+\sqrt{\mathrm{x}}} \\ $$$$=\frac{\mathrm{1}+\sqrt{\frac{\mathrm{1}}{\mathrm{x}}+\sqrt{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }}}}{\mathrm{1}+\sqrt{\frac{\mathrm{1}}{\mathrm{x}}}}\rightarrow\mathrm{1when}\:\mathrm{x}\rightarrow\infty \\ $$$$\Rightarrow\underset{\boldsymbol{\mathrm{x}}\rightarrow\infty} {\boldsymbol{\mathrm{lim}}}\left(\boldsymbol{\mathrm{y}}^{\mathrm{2}} \right)=\mathrm{1}\Rightarrow\underset{\boldsymbol{\mathrm{x}}\rightarrow\infty} {\boldsymbol{\mathrm{lim}y}}=\mathrm{1}\:\left(\boldsymbol{\mathrm{as}}\:\boldsymbol{\mathrm{y}}>\mathrm{0}\right) \\ $$
