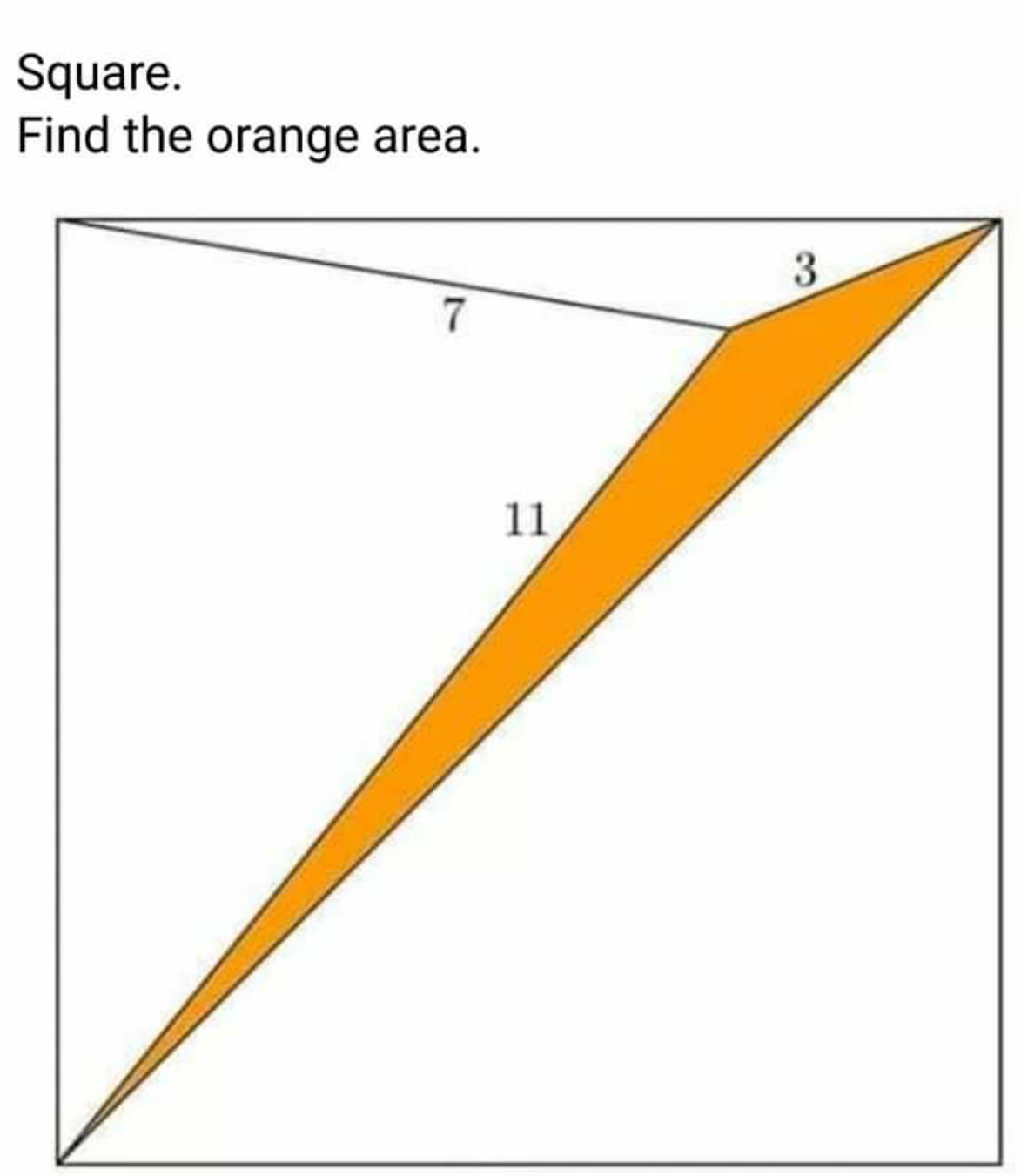
Question Number 108332 by I want to learn more last updated on 16/Aug/20
Answered by mr W last updated on 16/Aug/20
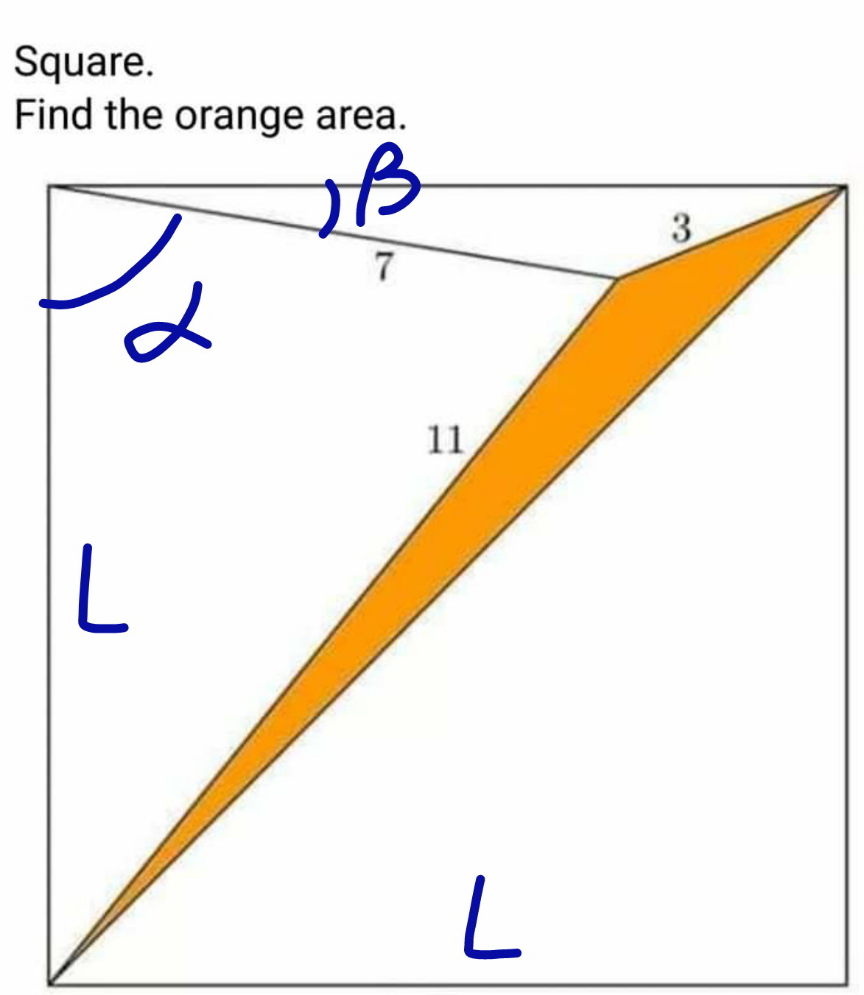
Commented by mr W last updated on 16/Aug/20
![cos α=((L^2 +7^2 −11^2 )/(2×7×L)) sin α=cos β=((L^2 +7^2 −3^2 )/(2×7×L)) (((L^2 +7^2 −11^2 )/(2×7×L)))^2 +(((L^2 +7^2 −3^2 )/(2×7×L)))^2 =1 L^4 −(11^2 +3^2 )L^2 +(((7^2 −11^2 )^2 +(7^2 −3^3 )^2 )/2)=0 ⇒L^2 =(1/2)[11^2 +3^2 +(√((11^2 +3^2 )^2 −2(7^2 −11^2 )^2 −2(7^2 −3^2 )^2 ))]=65+7(√(17)) ⇒L=(√(65+7(√(17)))) cos α=((L^2 +7^2 −11^2 )/(2×7×L))=(((√(17))−1)/( 2(√(65+7(√(17)))))) sin α=((L^2 +7^2 −3^2 )/(2×7×L))=((15+(√(17)))/( 2(√(65+7(√(17)))))) A_(orange) =(L^2 /2)−((L×7)/2)(sin α+cos α) =((65+7(√(17)))/2)−(7/2)×((((√(17))−1)/2)+((15+(√(17)))/2)) =8](https://www.tinkutara.com/question/Q108342.png)
$$\mathrm{cos}\:\alpha=\frac{{L}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} −\mathrm{11}^{\mathrm{2}} }{\mathrm{2}×\mathrm{7}×{L}} \\ $$$$\mathrm{sin}\:\alpha=\mathrm{cos}\:\beta=\frac{{L}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} }{\mathrm{2}×\mathrm{7}×{L}} \\ $$$$\left(\frac{{L}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} −\mathrm{11}^{\mathrm{2}} }{\mathrm{2}×\mathrm{7}×{L}}\right)^{\mathrm{2}} +\left(\frac{{L}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} }{\mathrm{2}×\mathrm{7}×{L}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$${L}^{\mathrm{4}} −\left(\mathrm{11}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} \right){L}^{\mathrm{2}} +\frac{\left(\mathrm{7}^{\mathrm{2}} −\mathrm{11}^{\mathrm{2}} \right)^{\mathrm{2}} +\left(\mathrm{7}^{\mathrm{2}} −\mathrm{3}^{\mathrm{3}} \right)^{\mathrm{2}} }{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow{L}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{11}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +\sqrt{\left(\mathrm{11}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{7}^{\mathrm{2}} −\mathrm{11}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{7}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} \right)^{\mathrm{2}} }\right]=\mathrm{65}+\mathrm{7}\sqrt{\mathrm{17}} \\ $$$$\Rightarrow{L}=\sqrt{\mathrm{65}+\mathrm{7}\sqrt{\mathrm{17}}} \\ $$$$\mathrm{cos}\:\alpha=\frac{{L}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} −\mathrm{11}^{\mathrm{2}} }{\mathrm{2}×\mathrm{7}×{L}}=\frac{\sqrt{\mathrm{17}}−\mathrm{1}}{\:\mathrm{2}\sqrt{\mathrm{65}+\mathrm{7}\sqrt{\mathrm{17}}}} \\ $$$$\mathrm{sin}\:\alpha=\frac{{L}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} }{\mathrm{2}×\mathrm{7}×{L}}=\frac{\mathrm{15}+\sqrt{\mathrm{17}}}{\:\mathrm{2}\sqrt{\mathrm{65}+\mathrm{7}\sqrt{\mathrm{17}}}} \\ $$$${A}_{{orange}} =\frac{{L}^{\mathrm{2}} }{\mathrm{2}}−\frac{{L}×\mathrm{7}}{\mathrm{2}}\left(\mathrm{sin}\:\alpha+\mathrm{cos}\:\alpha\right) \\ $$$$=\frac{\mathrm{65}+\mathrm{7}\sqrt{\mathrm{17}}}{\mathrm{2}}−\frac{\mathrm{7}}{\mathrm{2}}×\left(\frac{\sqrt{\mathrm{17}}−\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{15}+\sqrt{\mathrm{17}}}{\mathrm{2}}\right) \\ $$$$=\mathrm{8} \\ $$
Commented by I want to learn more last updated on 16/Aug/20
$$\mathrm{Wow},\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir} \\ $$
