Question Number 108365 by mathdave last updated on 16/Aug/20
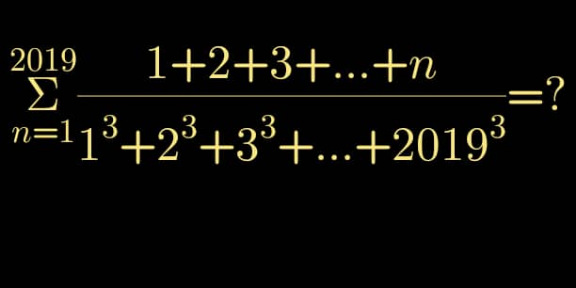
Answered by JDamian last updated on 16/Aug/20
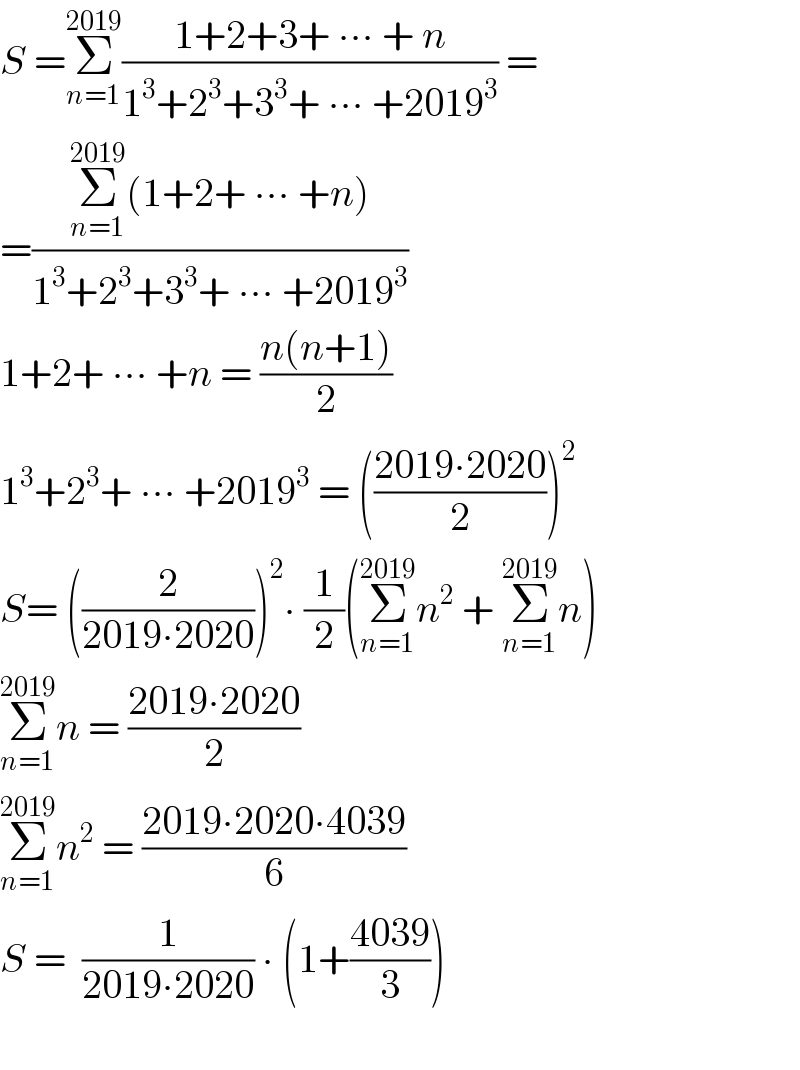
$${S}\:=\underset{{n}=\mathrm{1}} {\overset{\mathrm{2019}} {\sum}}\frac{\mathrm{1}+\mathrm{2}+\mathrm{3}+\:\centerdot\centerdot\centerdot\:+\:{n}}{\mathrm{1}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} +\mathrm{3}^{\mathrm{3}} +\:\centerdot\centerdot\centerdot\:+\mathrm{2019}^{\mathrm{3}} }\:= \\ $$$$=\frac{\underset{{n}=\mathrm{1}} {\overset{\mathrm{2019}} {\sum}}\left(\mathrm{1}+\mathrm{2}+\:\centerdot\centerdot\centerdot\:+{n}\right)}{\mathrm{1}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} +\mathrm{3}^{\mathrm{3}} +\:\centerdot\centerdot\centerdot\:+\mathrm{2019}^{\mathrm{3}} }\: \\ $$$$\mathrm{1}+\mathrm{2}+\:\centerdot\centerdot\centerdot\:+{n}\:=\:\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\mathrm{1}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} +\:\centerdot\centerdot\centerdot\:+\mathrm{2019}^{\mathrm{3}} \:=\:\left(\frac{\mathrm{2019}\centerdot\mathrm{2020}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${S}=\:\left(\frac{\mathrm{2}}{\mathrm{2019}\centerdot\mathrm{2020}}\right)^{\mathrm{2}} \centerdot\:\frac{\mathrm{1}}{\mathrm{2}}\left(\underset{{n}=\mathrm{1}} {\overset{\mathrm{2019}} {\sum}}{n}^{\mathrm{2}} \:+\:\underset{{n}=\mathrm{1}} {\overset{\mathrm{2019}} {\sum}}{n}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{2019}} {\sum}}{n}\:=\:\frac{\mathrm{2019}\centerdot\mathrm{2020}}{\mathrm{2}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{2019}} {\sum}}{n}^{\mathrm{2}} \:=\:\frac{\mathrm{2019}\centerdot\mathrm{2020}\centerdot\mathrm{4039}}{\mathrm{6}} \\ $$$${S}\:=\:\:\frac{\mathrm{1}}{\mathrm{2019}\centerdot\mathrm{2020}}\:\centerdot\:\left(\mathrm{1}+\frac{\mathrm{4039}}{\mathrm{3}}\right) \\ $$$$ \\ $$
