Question-108417

Question Number 108417 by mathdave last updated on 16/Aug/20

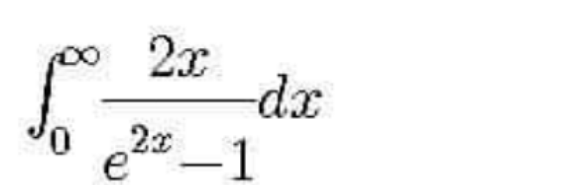
Answered by Aziztisffola last updated on 16/Aug/20

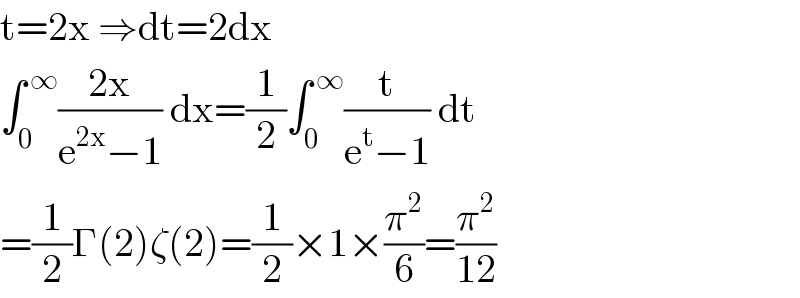
t=2x ⇒dt=2dx ∫_0 ^( ∞) ((2x)/(e^(2x) −1)) dx=(1/2)∫_0 ^( ∞) (t/(e^t −1)) dt =(1/2)Γ(2)ζ(2)=(1/2)×1×(π^2 /6)=(π^2 /(12))

$$\mathrm{t}=\mathrm{2x}\:\Rightarrow\mathrm{dt}=\mathrm{2dx} \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{2x}}{\mathrm{e}^{\mathrm{2x}} −\mathrm{1}}\:\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{t}}{\mathrm{e}^{\mathrm{t}} −\mathrm{1}}\:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\mathrm{2}\right)\zeta\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{1}×\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$

Answered by mnjuly1970 last updated on 16/Aug/20

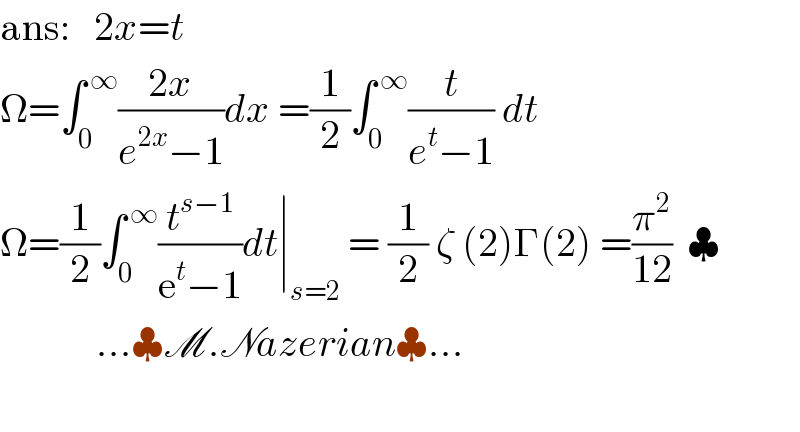
ans: 2x=t Ω=∫_0 ^( ∞) ((2x)/(e^(2x) −1))dx =(1/2)∫_0 ^( ∞) (t/(e^t −1)) dt Ω=(1/2)∫_0 ^( ∞) (t^(s−1) /(e^t −1))dt∣_(s=2) = (1/2) ζ (2)Γ(2) =(π^2 /(12)) ♣ ...♣M.Nazerian♣...

$$\mathrm{ans}:\:\:\:\mathrm{2}{x}={t} \\ $$$$\Omega=\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{2}{x}}{{e}^{\mathrm{2}{x}} −\mathrm{1}}{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \frac{{t}}{{e}^{{t}} −\mathrm{1}}\:{dt} \\ $$$$\Omega=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \frac{{t}^{{s}−\mathrm{1}} }{\mathrm{e}^{{t}} −\mathrm{1}}{dt}\mid_{{s}=\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\zeta\:\left(\mathrm{2}\right)\Gamma\left(\mathrm{2}\right)\:=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:\:\clubsuit\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:…\clubsuit\mathscr{M}.\mathscr{N}{azerian}\clubsuit… \\ $$$$ \\ $$

Answered by mathmax by abdo last updated on 16/Aug/20

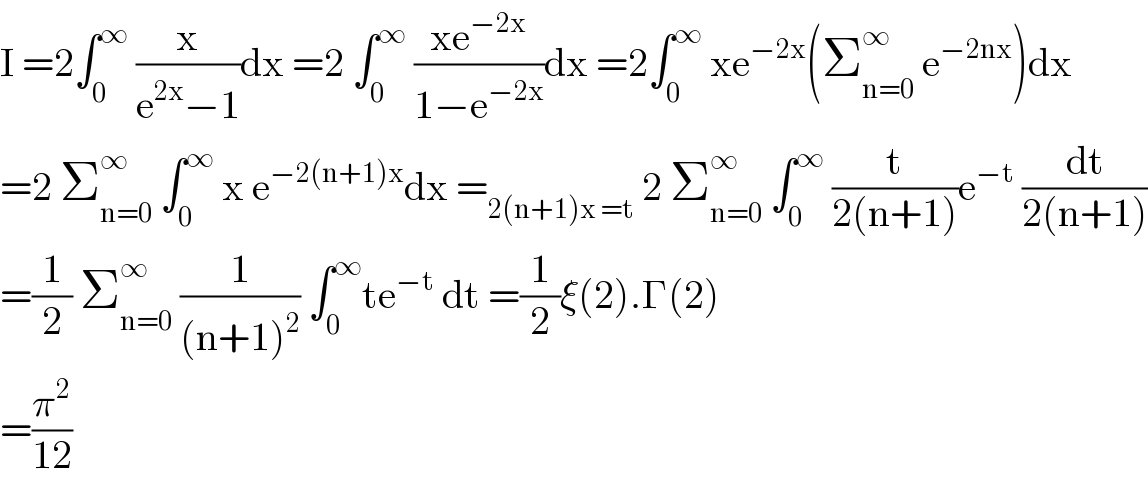
I =2∫_0 ^∞ (x/(e^(2x) −1))dx =2 ∫_0 ^∞ ((xe^(−2x) )/(1−e^(−2x) ))dx =2∫_0 ^∞ xe^(−2x) (Σ_(n=0) ^∞ e^(−2nx) )dx =2 Σ_(n=0) ^∞ ∫_0 ^∞ x e^(−2(n+1)x) dx =_(2(n+1)x =t) 2 Σ_(n=0) ^∞ ∫_0 ^∞ (t/(2(n+1)))e^(−t) (dt/(2(n+1))) =(1/2) Σ_(n=0) ^(∞ ) (1/((n+1)^2 )) ∫_0 ^∞ te^(−t) dt =(1/2)ξ(2).Γ(2) =(π^2 /(12))

$$\mathrm{I}\:=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}}{\mathrm{e}^{\mathrm{2x}} −\mathrm{1}}\mathrm{dx}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{xe}^{−\mathrm{2x}} }{\mathrm{1}−\mathrm{e}^{−\mathrm{2x}} }\mathrm{dx}\:=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\mathrm{xe}^{−\mathrm{2x}} \left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{2nx}} \right)\mathrm{dx} \\ $$$$=\mathrm{2}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\infty} \:\mathrm{x}\:\mathrm{e}^{−\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}} \mathrm{dx}\:=_{\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}\:=\mathrm{t}} \:\mathrm{2}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}}{\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)}\mathrm{e}^{−\mathrm{t}} \:\frac{\mathrm{dt}}{\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty\:} \:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\infty} \mathrm{te}^{−\mathrm{t}} \:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\xi\left(\mathrm{2}\right).\Gamma\left(\mathrm{2}\right) \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply