Question Number 108420 by mathdave last updated on 16/Aug/20

Answered by prakash jain last updated on 18/Sep/20

$$−−−−−−−−−−−−−−−− \\ $$$$\mathrm{12}+\mathrm{3}=\mathrm{15}\:\mathrm{dashes} \\ $$$$\mathrm{select}\:\mathrm{3}\:\mathrm{dashes}\:\mathrm{and}\:\mathrm{change}\:\mathrm{them}\:\mathrm{to} \\ $$$$\mathrm{bar}\:\mathrm{it}\:\mathrm{will}\:\mathrm{create}\:\mathrm{four}\:\mathrm{partions} \\ $$$$\mathrm{with}\:\mathrm{total}\:\mathrm{number}\:\mathrm{of}\:\mathrm{dashes}=\mathrm{12} \\ $$$$\:^{\mathrm{15}} \mathrm{C}_{\mathrm{3}} \\ $$
Answered by ajfour last updated on 17/Aug/20
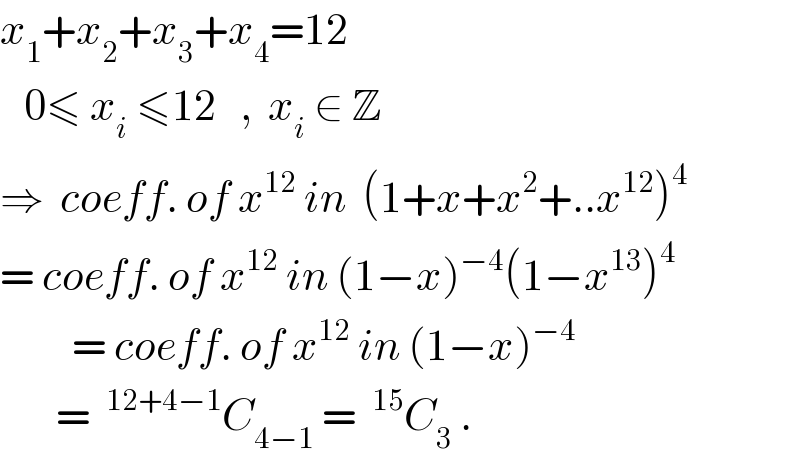
$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +{x}_{\mathrm{4}} =\mathrm{12} \\ $$$$\:_{} \:\:\mathrm{0}\leqslant\:{x}_{{i}} \:\leqslant\mathrm{12}\:\:\:,\:\:{x}_{{i}} \:\in\:\mathbb{Z} \\ $$$$\Rightarrow\:\:{coeff}.\:{of}\:{x}^{\mathrm{12}} \:{in}\:\:\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +..{x}^{\mathrm{12}} \right)^{\mathrm{4}} \\ $$$$=\:{coeff}.\:{of}\:{x}^{\mathrm{12}} \:{in}\:\left(\mathrm{1}−{x}\right)^{−\mathrm{4}} \left(\mathrm{1}−{x}^{\mathrm{13}} \right)^{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:=\:{coeff}.\:{of}\:{x}^{\mathrm{12}} \:{in}\:\left(\mathrm{1}−{x}\right)^{−\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:=\:\:^{\mathrm{12}+\mathrm{4}−\mathrm{1}} {C}_{\mathrm{4}−\mathrm{1}} \:=\:\:^{\mathrm{15}} {C}_{\mathrm{3}} \:. \\ $$
