Question Number 108422 by maouame last updated on 16/Aug/20
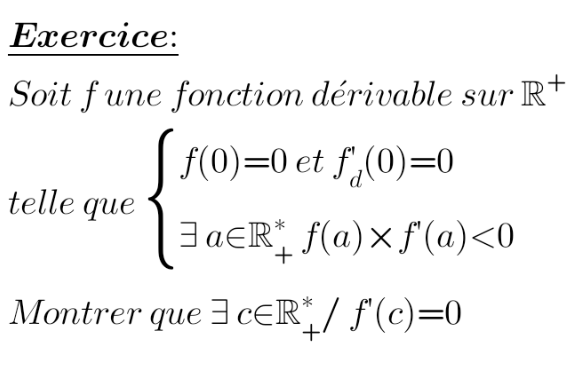
Answered by bubugne last updated on 17/Aug/20
![1 − solution triviale ∃ ε ∈ R_+ ^∗ ∀ c ∈ ]0,ε] f(c)=f ′(c)=0 2 − solution non triviale f(0)=0 et f ′(0)=0 ⇒ ∃ ε ∈ R_+ ^∗ ∀ x ∈ ]0,ε] f ′(x)≠0 et f(x)×f ′(x)>0 {: ((∃ ε ∈ R_+ ^∗ ∀ x ∈ ]0,ε] f(x)×f ′(x)>0)),((∃ a ∈ R_+ ^∗ f(a)×f ′(a)<0)) } ⇒ ∃ c ∈ ]ε,a[ f ′(c)=0](https://www.tinkutara.com/question/Q108435.png)
$$ \\ $$$$\mathrm{1}\:−\:{solution}\:{triviale}\: \\ $$$$\left.\exists\left.\:\epsilon\:\in\:\mathbb{R}_{+} ^{\ast} \:\forall\:{c}\:\in\:\right]\mathrm{0},\epsilon\right]\:{f}\left({c}\right)={f}\:'\left({c}\right)=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{2}\:−\:{solution}\:{non}\:{triviale} \\ $$$$\left.{f}\left.\left(\mathrm{0}\right)=\mathrm{0}\:{et}\:{f}\:'\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow\:\exists\:\epsilon\:\in\:\mathbb{R}_{+} ^{\ast} \:\forall\:{x}\:\in\:\right]\mathrm{0},\epsilon\right]\:{f}\:'\left({x}\right)\neq\mathrm{0}\:{et}\:{f}\left({x}\right)×{f}\:'\left({x}\right)>\mathrm{0} \\ $$$$\left.\left.\begin{matrix}{\left.\exists\left.\:\epsilon\:\in\:\mathbb{R}_{+} ^{\ast} \:\forall\:{x}\:\in\:\right]\mathrm{0},\epsilon\right]\:{f}\left({x}\right)×{f}\:'\left({x}\right)>\mathrm{0}}\\{\exists\:{a}\:\in\:\mathbb{R}_{+} ^{\ast} \:{f}\left({a}\right)×{f}\:'\left({a}\right)<\mathrm{0}}\end{matrix}\right\}\:\Rightarrow\:\exists\:{c}\:\in\:\right]\epsilon,{a}\left[\:{f}\:'\left({c}\right)=\mathrm{0}\right. \\ $$$$ \\ $$
