Question Number 108429 by Rasikh last updated on 16/Aug/20
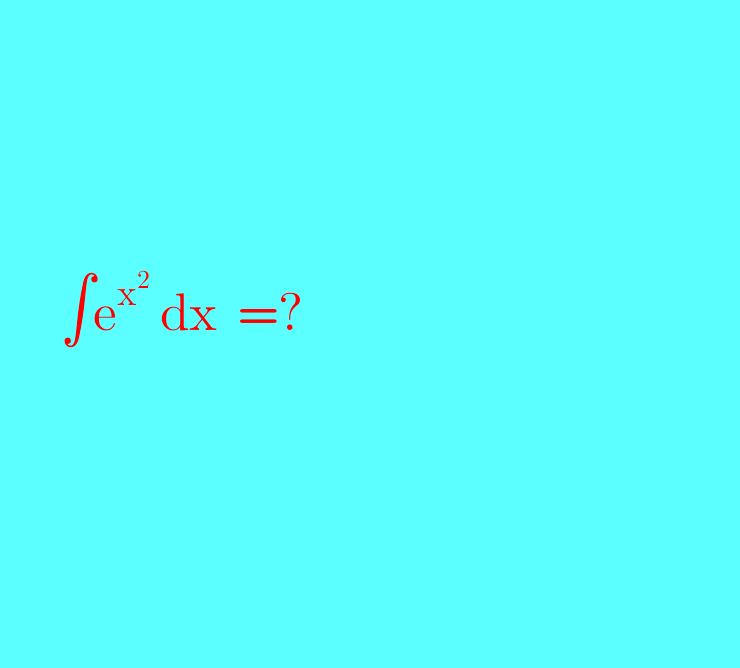
Answered by Sarah85 last updated on 17/Aug/20
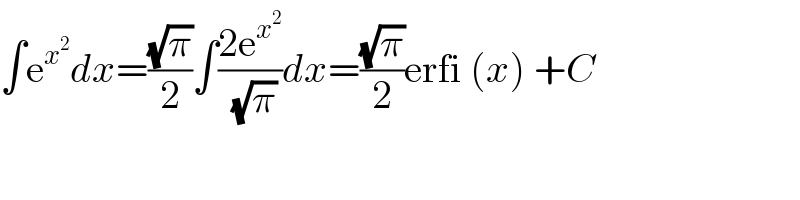
$$\int\mathrm{e}^{{x}^{\mathrm{2}} } {dx}=\frac{\sqrt{\pi}}{\mathrm{2}}\int\frac{\mathrm{2e}^{{x}^{\mathrm{2}} } }{\:\sqrt{\pi}}{dx}=\frac{\sqrt{\pi}}{\mathrm{2}}\mathrm{erfi}\:\left({x}\right)\:+{C} \\ $$
Commented by Rasikh last updated on 17/Aug/20
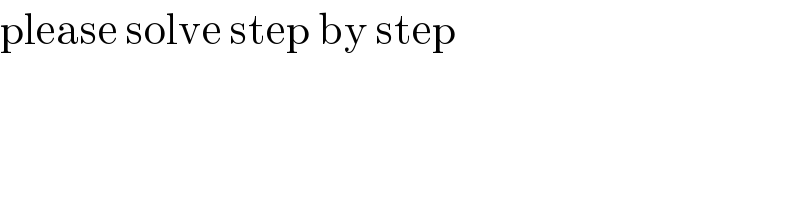
$$\mathrm{please}\:\mathrm{solve}\:\mathrm{step}\:\mathrm{by}\:\mathrm{step} \\ $$
Commented by Sarah85 last updated on 17/Aug/20
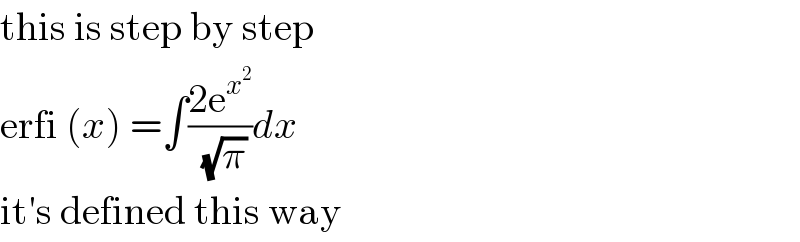
$$\mathrm{this}\:\mathrm{is}\:\mathrm{step}\:\mathrm{by}\:\mathrm{step} \\ $$$$\mathrm{erfi}\:\left({x}\right)\:=\int\frac{\mathrm{2e}^{{x}^{\mathrm{2}} } }{\:\sqrt{\pi}}{dx} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{defined}\:\mathrm{this}\:\mathrm{way} \\ $$
Commented by 1549442205PVT last updated on 17/Aug/20
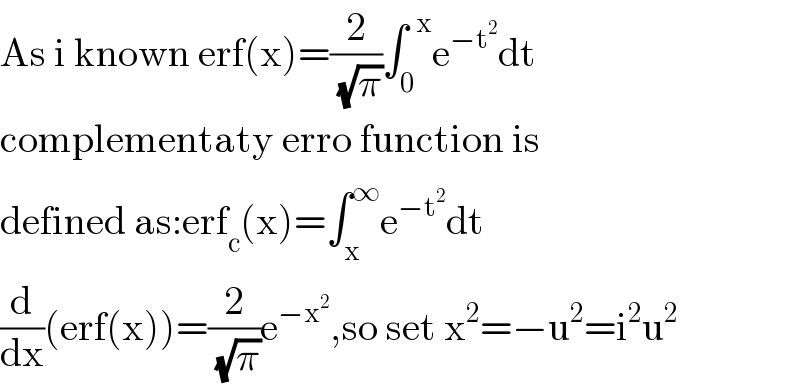
$$\mathrm{As}\:\mathrm{i}\:\mathrm{known}\:\mathrm{erf}\left(\mathrm{x}\right)=\frac{\mathrm{2}}{\:\sqrt{\pi}}\int_{\mathrm{0}} ^{\:\:\mathrm{x}} \mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dt} \\ $$$$\mathrm{complementaty}\:\mathrm{erro}\:\mathrm{function}\:\mathrm{is} \\ $$$$\mathrm{defined}\:\mathrm{as}:\mathrm{erf}_{\mathrm{c}} \left(\mathrm{x}\right)=\int_{\mathrm{x}} ^{\infty} \mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dt} \\ $$$$\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{erf}\left(\mathrm{x}\right)\right)=\frac{\mathrm{2}}{\:\sqrt{\pi}}\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } ,\mathrm{so}\:\mathrm{set}\:\mathrm{x}^{\mathrm{2}} =−\mathrm{u}^{\mathrm{2}} =\mathrm{i}^{\mathrm{2}} \mathrm{u}^{\mathrm{2}} \\ $$
Commented by Sarah85 last updated on 17/Aug/20
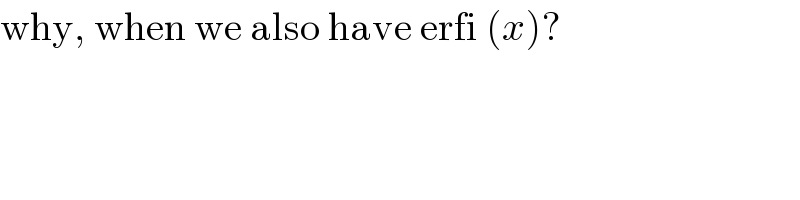
$$\mathrm{why},\:\mathrm{when}\:\mathrm{we}\:\mathrm{also}\:\mathrm{have}\:\mathrm{erfi}\:\left({x}\right)? \\ $$
