Question Number 108430 by Rasikh last updated on 16/Aug/20
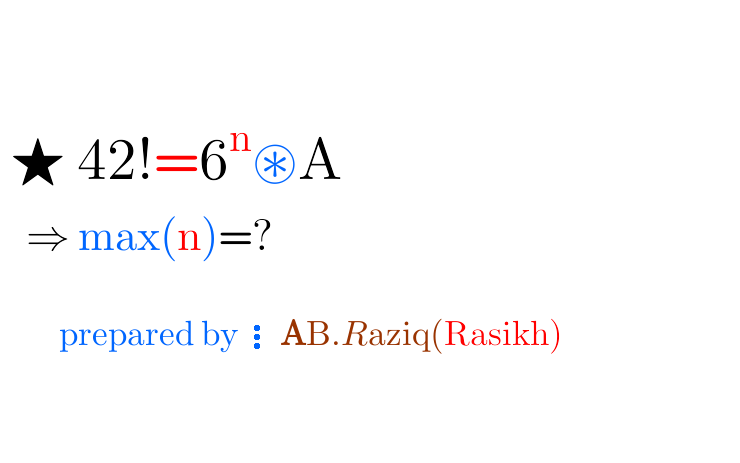
Answered by Sarah85 last updated on 17/Aug/20
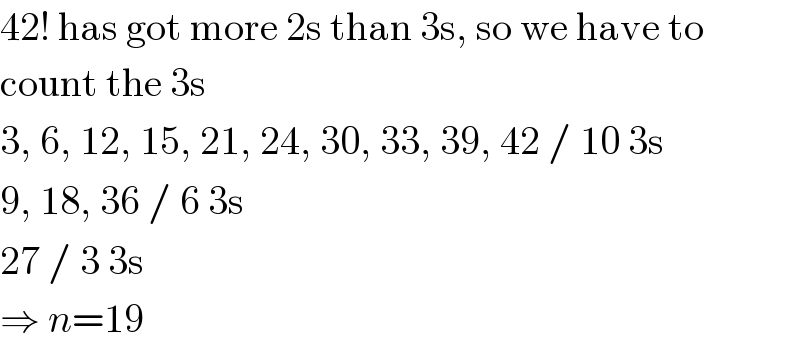
$$\mathrm{42}!\:\mathrm{has}\:\mathrm{got}\:\mathrm{more}\:\mathrm{2s}\:\mathrm{than}\:\mathrm{3s},\:\mathrm{so}\:\mathrm{we}\:\mathrm{have}\:\mathrm{to} \\ $$$$\mathrm{count}\:\mathrm{the}\:\mathrm{3s} \\ $$$$\mathrm{3},\:\mathrm{6},\:\mathrm{12},\:\mathrm{15},\:\mathrm{21},\:\mathrm{24},\:\mathrm{30},\:\mathrm{33},\:\mathrm{39},\:\mathrm{42}\:/\:\mathrm{10}\:\mathrm{3s} \\ $$$$\mathrm{9},\:\mathrm{18},\:\mathrm{36}\:/\:\mathrm{6}\:\mathrm{3s} \\ $$$$\mathrm{27}\:/\:\mathrm{3}\:\mathrm{3s} \\ $$$$\Rightarrow\:{n}=\mathrm{19} \\ $$
Commented by Rasikh last updated on 17/Aug/20

$$\mathrm{thans}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{sir} \\ $$
Commented by udaythool last updated on 17/Aug/20

$$\mathrm{There}\:\mathrm{are}\:\mathrm{14}\:\mathrm{no}.\mathrm{s}\:\mathrm{which}\:\mathrm{are} \\ $$$$\mathrm{multiple}\:\mathrm{of}\:\mathrm{3},\:\mathrm{4}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{9}\:\mathrm{and} \\ $$$$\mathrm{1}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{27}. \\ $$$$\mathrm{Therefore}\:\mathrm{42}!\:\mathrm{is}\:\mathrm{a}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{3}^{\mathrm{14}+\mathrm{4}+\mathrm{1}} =\mathrm{3}^{\mathrm{19}} . \\ $$$$\mathrm{No}\:\mathrm{doubt}\:\mathrm{42}!\:\mathrm{is}\:\mathrm{a}\:\mathrm{multiple}\:\mathrm{of} \\ $$$$\mathrm{more}\:\mathrm{than}\:\mathrm{19th}\:\mathrm{power}\:\mathrm{of}\:\mathrm{2}.\:\mathrm{Thus} \\ $$$$\mathrm{42}!\:\mathrm{is}\:\mathrm{a}\:\mathrm{multiple}\:\mathrm{of} \\ $$$$\mathrm{19th}\:\mathrm{power}\:\mathrm{of}\:\mathrm{6},\:\mathrm{since}\:\mathrm{2}\:\mathrm{and}\:\mathrm{3} \\ $$$$\mathrm{are}\:\mathrm{relatively}\:\mathrm{prime}. \\ $$
Commented by Rasikh last updated on 18/Aug/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
