Question Number 108456 by Khalmohmmad last updated on 17/Aug/20
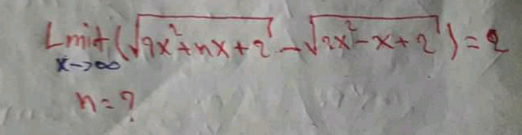
Commented by Rizwankhan last updated on 17/Aug/20
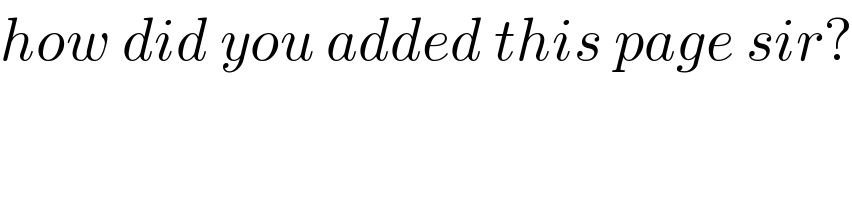
$${how}\:{did}\:{you}\:{added}\:{this}\:{page}\:{sir}? \\ $$
Answered by bemath last updated on 17/Aug/20
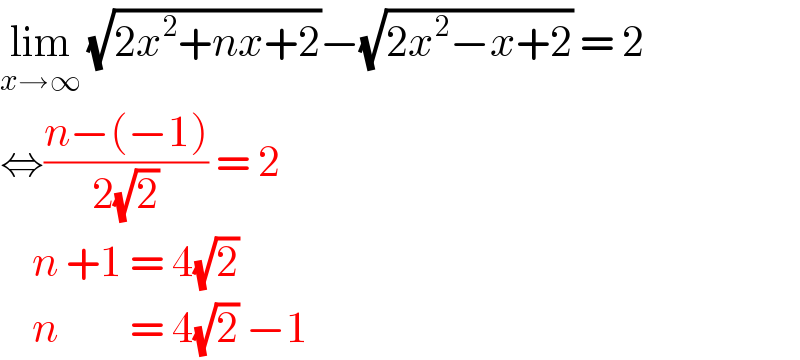
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{2}{x}^{\mathrm{2}} +{nx}+\mathrm{2}}−\sqrt{\mathrm{2}{x}^{\mathrm{2}} −{x}+\mathrm{2}}\:=\:\mathrm{2} \\ $$$$\Leftrightarrow\frac{{n}−\left(−\mathrm{1}\right)}{\mathrm{2}\sqrt{\mathrm{2}}}\:=\:\mathrm{2}\: \\ $$$$\:\:\:\:{n}\:+\mathrm{1}\:=\:\mathrm{4}\sqrt{\mathrm{2}} \\ $$$$\:\:\:\:{n}\:\:\:\:\:\:\:\:\:=\:\mathrm{4}\sqrt{\mathrm{2}}\:−\mathrm{1} \\ $$
Answered by Dwaipayan Shikari last updated on 17/Aug/20
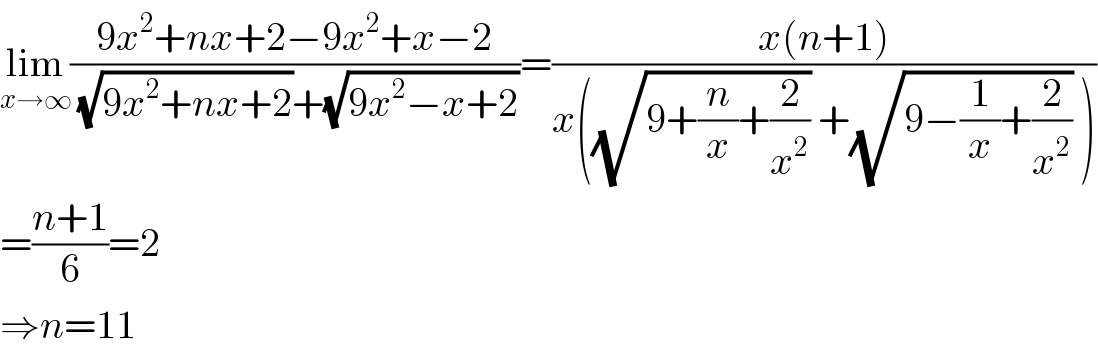
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{9}{x}^{\mathrm{2}} +{nx}+\mathrm{2}−\mathrm{9}{x}^{\mathrm{2}} +{x}−\mathrm{2}}{\:\sqrt{\mathrm{9}{x}^{\mathrm{2}} +{nx}+\mathrm{2}}+\sqrt{\mathrm{9}{x}^{\mathrm{2}} −{x}+\mathrm{2}}}=\frac{{x}\left({n}+\mathrm{1}\right)}{{x}\left(\sqrt{\mathrm{9}+\frac{{n}}{{x}}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} }}\:+\sqrt{\mathrm{9}−\frac{\mathrm{1}}{{x}}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} }}\:\right)} \\ $$$$=\frac{{n}+\mathrm{1}}{\mathrm{6}}=\mathrm{2} \\ $$$$\Rightarrow{n}=\mathrm{11} \\ $$
Commented by bemath last updated on 17/Aug/20
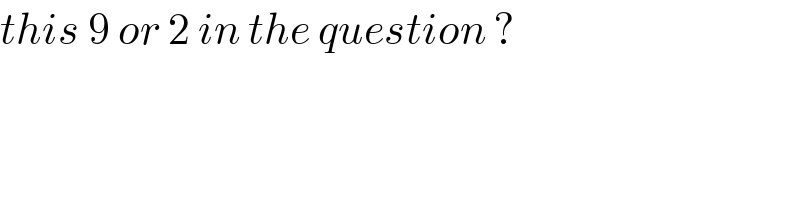
$${this}\:\mathrm{9}\:{or}\:\mathrm{2}\:{in}\:{the}\:{question}\:? \\ $$
Commented by Aziztisffola last updated on 17/Aug/20

$$\mathrm{It}\:\mathrm{looks}\:\mathrm{like}\:\mathrm{9}\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{clear}. \\ $$
Answered by Aziztisffola last updated on 17/Aug/20
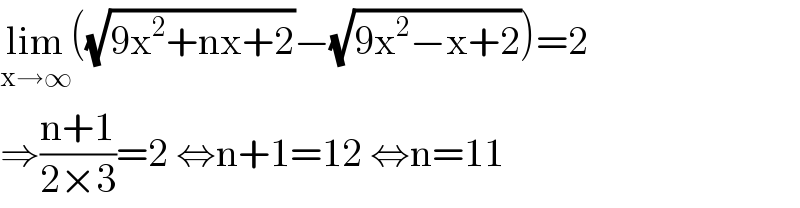
$$\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\left(\sqrt{\mathrm{9x}^{\mathrm{2}} +\mathrm{nx}+\mathrm{2}}−\sqrt{\mathrm{9x}^{\mathrm{2}} −\mathrm{x}+\mathrm{2}}\right)=\mathrm{2} \\ $$$$\Rightarrow\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}×\mathrm{3}}=\mathrm{2}\:\Leftrightarrow\mathrm{n}+\mathrm{1}=\mathrm{12}\:\Leftrightarrow\mathrm{n}=\mathrm{11} \\ $$
