Menu Close

Question-108480

Tinku Tara 0 Comments
Pin




Question Number 108480 by I want to learn more last updated on 17/Aug/20
Answered by Rasheed.Sindhi last updated on 17/Aug/20
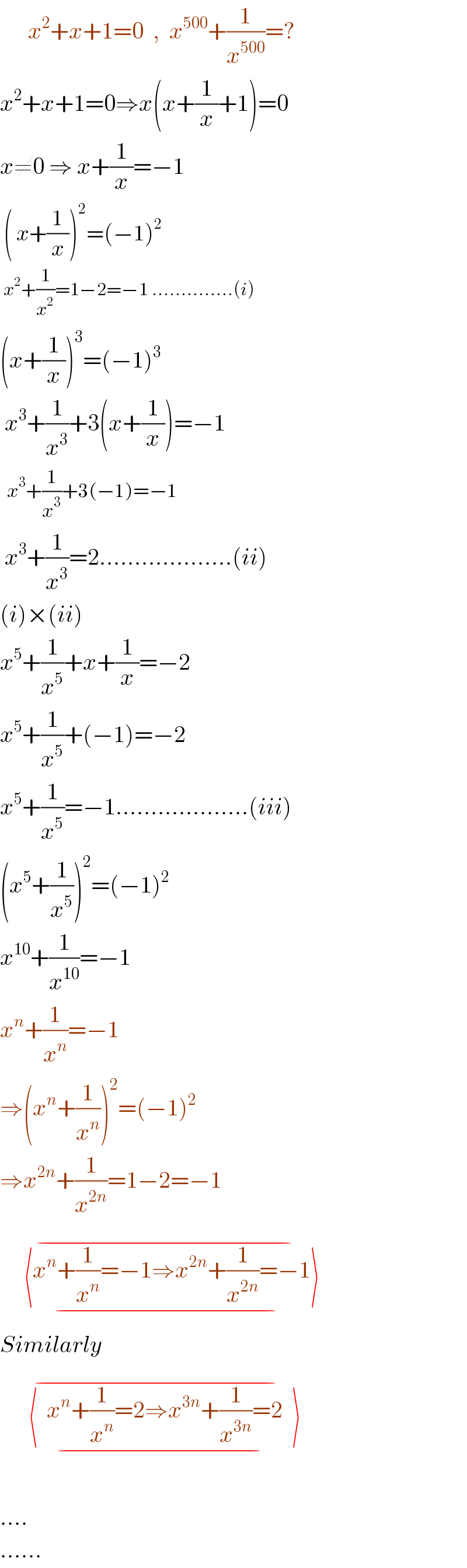
x^2 +x+1=0 , x^(500) +(1/x^(500) )=? x^2 +x+1=0⇒x(x+(1/x)+1)=0 x≠0 ⇒ x+(1/x)=−1 ( x+(1/x))^2 =(−1)^2 x^2 +(1/x^2 )=1−2=−1 ..............(i) (x+(1/x))^3 =(−1)^3 x^3 +(1/x^3 )+3(x+(1/x))=−1 x^3 +(1/x^3 )+3(−1)=−1 x^3 +(1/x^3 )=2...................(ii) (i)×(ii) x^5 +(1/x^5 )+x+(1/x)=−2 x^5 +(1/x^5 )+(−1)=−2 x^5 +(1/x^5 )=−1...................(iii) (x^5 +(1/x^5 ))^2 =(−1)^2 x^(10) +(1/x^(10) )=−1 x^n +(1/x^n )=−1 ⇒(x^n +(1/x^n ))^2 =(−1)^2 ⇒x^(2n) +(1/x^(2n) )=1−2=−1 ⟨x^n +(1/x^n )=−1⇒x^(2n) +(1/x^(2n) )=−1⟩_(−) ^(−) Similarly ⟨ x^n +(1/x^n )=2⇒x^(3n) +(1/x^(3n) )=2 ⟩_(−) ^(−) .... ......
$$\:\:\:\:\:\:{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0}\:\:,\:\:{x}^{\mathrm{500}} +\frac{\mathrm{1}}{{x}^{\mathrm{500}} }=? \\ $$$${x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0}\Rightarrow{x}\left({x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}\neq\mathrm{0}\:\Rightarrow\:{x}+\frac{\mathrm{1}}{{x}}=−\mathrm{1} \\ $$$$\:\left(\:{x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} =\left(−\mathrm{1}\right)^{\mathrm{2}} \:\:\: \\ $$$$\:{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{1}−\mathrm{2}=−\mathrm{1}\:…………..\left({i}\right) \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{3}} =\left(−\mathrm{1}\right)^{\mathrm{3}} \\ $$$$\:{x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }+\mathrm{3}\left({x}+\frac{\mathrm{1}}{{x}}\right)=−\mathrm{1} \\ $$$$\:\:{x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }+\mathrm{3}\left(−\mathrm{1}\right)=−\mathrm{1} \\ $$$$\:{x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }=\mathrm{2}……………….\left({ii}\right) \\ $$$$\left({i}\right)×\left({ii}\right) \\ $$$${x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }+{x}+\frac{\mathrm{1}}{{x}}=−\mathrm{2} \\ $$$${x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }+\left(−\mathrm{1}\right)=−\mathrm{2} \\ $$$${x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }=−\mathrm{1}……………….\left({iii}\right) \\ $$$$\left({x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }\right)^{\mathrm{2}} =\left(−\mathrm{1}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{10}} +\frac{\mathrm{1}}{{x}^{\mathrm{10}} }=−\mathrm{1} \\ $$$${x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }=−\mathrm{1} \\ $$$$\Rightarrow\left({x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }\right)^{\mathrm{2}} =\left(−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{x}^{\mathrm{2}{n}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}{n}} }=\mathrm{1}−\mathrm{2}=−\mathrm{1} \\ $$$$\overline {\:\:\:\:\:\langle{x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }=−\mathrm{1}\Rightarrow{x}^{\mathrm{2}{n}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}{n}} }=−\mathrm{1}\rangle\:\:\:\:\:} \\ $$$${Similarly} \\ $$$$\overline {\:\:\:\:\:\:\langle\:\:{x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }=\mathrm{2}\Rightarrow{x}^{\mathrm{3}{n}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}{n}} }=\mathrm{2}\:\:\rangle\:\:\:\:\:} \\ $$$$ \\ $$$$…. \\ $$$$…… \\ $$
Commented by I want to learn more last updated on 17/Aug/20
Thanks sir, i appreciate
$$\mathrm{Thanks}\:\mathrm{sir},\:\:\mathrm{i}\:\mathrm{appreciate} \\ $$
Commented by udaythool last updated on 17/Aug/20
supper
$$\mathrm{supper} \\ $$
Answered by 1549442205PVT last updated on 17/Aug/20
From the hypothesis we get x^2 +x+1=0 Δ=1−4=−3=3i^2 ⇒x=((−1±i(√3))/2)=cos((2π)/3)±isin((2π)/3) ⇒x^(500) =(cos((2π)/3)±isin((2π)/3))^(500) =cos((1000π)/3)±sin((1000π)/3)=cos(333π+(π/3))±isin(333π+(π/3)) =−cos(π/3)∓isin(π/3)=−(1/2)∓i((√3)/2) =((−1∓i(√3))/2)(1) ⇒(1/x^(500) )=(2/(−1∓i(√3)))=((2(−1±i(√3)))/((−1)^2 −(i(√3))^2 ))=((2(−1±i(√3)))/(1−3i^2 )) =((2(−1±i(√3)))/4)=((−1±i(√3))/2)(2) Adding up two the eqialities (1) (2) we get x^(500) +(1/x^(500) )=((−1∓i(√3)+−1±i(√3))/2)=−1 Thus,x^(500) +(1/x^(500) )=((−2)/2)=−1.
$$\mathrm{From}\:\mathrm{the}\:\mathrm{hypothesis}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}=\mathrm{0}\:\Delta=\mathrm{1}−\mathrm{4}=−\mathrm{3}=\mathrm{3i}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{x}=\frac{−\mathrm{1}\pm\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{cos}\frac{\mathrm{2}\pi}{\mathrm{3}}\pm\mathrm{isin}\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{500}} =\left(\mathrm{cos}\frac{\mathrm{2}\pi}{\mathrm{3}}\pm\mathrm{isin}\frac{\mathrm{2}\pi}{\mathrm{3}}\right)^{\mathrm{500}} \\ $$$$=\mathrm{cos}\frac{\mathrm{1000}\pi}{\mathrm{3}}\pm\mathrm{sin}\frac{\mathrm{1000}\pi}{\mathrm{3}}=\mathrm{cos}\left(\mathrm{333}\pi+\frac{\pi}{\mathrm{3}}\right)\pm\mathrm{isin}\left(\mathrm{333}\pi+\frac{\pi}{\mathrm{3}}\right) \\ $$$$=−\mathrm{cos}\frac{\pi}{\mathrm{3}}\mp\mathrm{isin}\frac{\pi}{\mathrm{3}}=−\frac{\mathrm{1}}{\mathrm{2}}\mp\mathrm{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$=\frac{−\mathrm{1}\mp\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\mathrm{1}\right) \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{500}} }=\frac{\mathrm{2}}{−\mathrm{1}\mp\mathrm{i}\sqrt{\mathrm{3}}}=\frac{\mathrm{2}\left(−\mathrm{1}\pm\mathrm{i}\sqrt{\mathrm{3}}\right)}{\left(−\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }=\frac{\mathrm{2}\left(−\mathrm{1}\pm\mathrm{i}\sqrt{\mathrm{3}}\right)}{\mathrm{1}−\mathrm{3i}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}\left(−\mathrm{1}\pm\mathrm{i}\sqrt{\mathrm{3}}\right)}{\mathrm{4}}=\frac{−\mathrm{1}\pm\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\mathrm{2}\right) \\ $$$$\mathrm{Adding}\:\mathrm{up}\:\mathrm{two}\:\mathrm{the}\:\mathrm{eqialities}\:\left(\mathrm{1}\right)\:\left(\mathrm{2}\right) \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{x}^{\mathrm{500}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{500}} }=\frac{−\mathrm{1}\mp\mathrm{i}\sqrt{\mathrm{3}}+−\mathrm{1}\pm\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}=−\mathrm{1} \\ $$$$\mathrm{Thus},\boldsymbol{\mathrm{x}}^{\mathrm{500}} +\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}^{\mathrm{500}} }=\frac{−\mathrm{2}}{\mathrm{2}}=−\mathrm{1}. \\ $$
Commented by I want to learn more last updated on 17/Aug/20
Thanks sir
$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Answered by Dwaipayan Shikari last updated on 17/Aug/20
x^2 +x+1=0 x=e^((2iπ)/3) or e^(−((2iπ)/3)) x^(500) =e^((1000iπ)/3) =e^(−((2πi)/3)) =−((1/2)+((√3)/2)i) (1/x^(500) )=e^((−1000πi)/3) =e^((2iπ)/3) =−(1/2)+((√3)/2)i x^(500) +(1/x^(500) )=−1 Or x^(500) =e^(−((1000iπ)/3)) (1/x^(500) )=e^((1000iπ)/3) x^(500) +(1/x^(500) )=−1
$${x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}={e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} \:{or}\:{e}^{−\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} \\ $$$${x}^{\mathrm{500}} ={e}^{\frac{\mathrm{1000}{i}\pi}{\mathrm{3}}} ={e}^{−\frac{\mathrm{2}\pi{i}}{\mathrm{3}}} =−\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}\right) \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{500}} }={e}^{\frac{−\mathrm{1000}\pi{i}}{\mathrm{3}}} ={e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} =−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i} \\ $$$${x}^{\mathrm{500}} +\frac{\mathrm{1}}{{x}^{\mathrm{500}} }=−\mathrm{1} \\ $$$${Or} \\ $$$${x}^{\mathrm{500}} ={e}^{−\frac{\mathrm{1000}{i}\pi}{\mathrm{3}}} \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{500}} }={e}^{\frac{\mathrm{1000}{i}\pi}{\mathrm{3}}} \\ $$$${x}^{\mathrm{500}} +\frac{\mathrm{1}}{{x}^{\mathrm{500}} }=−\mathrm{1} \\ $$$$ \\ $$
Commented by udaythool last updated on 17/Aug/20
excellent
$$\mathrm{excellent} \\ $$
Commented by I want to learn more last updated on 17/Aug/20
Thanks sir
$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Answered by mnjuly1970 last updated on 17/Aug/20
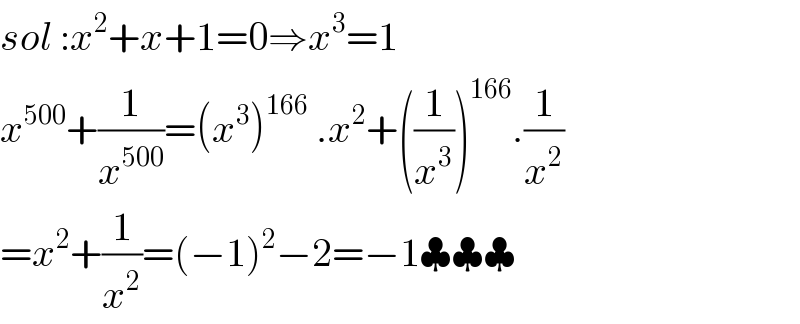
sol :x^2 +x+1=0⇒x^3 =1 x^(500) +(1/x^(500) )=(x^3 )^(166) .x^2 +((1/x^3 ))^(166) .(1/x^2 ) =x^2 +(1/x^2 )=(−1)^2 −2=−1♣♣♣
$${sol}\::{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0}\Rightarrow{x}^{\mathrm{3}} =\mathrm{1} \\ $$$${x}^{\mathrm{500}} +\frac{\mathrm{1}}{{x}^{\mathrm{500}} }=\left({x}^{\mathrm{3}} \right)^{\mathrm{166}} \:.{x}^{\mathrm{2}} +\left(\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)^{\mathrm{166}} .\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$$={x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\left(−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}=−\mathrm{1}\clubsuit\clubsuit\clubsuit \\ $$
Commented by I want to learn more last updated on 17/Aug/20
Thanks sir
$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 17/Aug/20
x^2 +x+1=0 x=((−1±(√(1−4)))/2)=((−1±i(√3))/2) x=ω,ω^2 x^(500) +(1/x^(500) )=ω^(500) +(1/ω^(500) ) (ω^3 )^(166) .ω^2 +(1/((ω^3 )^(166) .ω^2 )) =ω^2 +(1/ω^2 )×(ω/ω)=ω^2 +(ω/ω^3 )=ω^2 +ω=−1
$${x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{4}}}{\mathrm{2}}=\frac{−\mathrm{1}\pm{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${x}=\omega,\omega^{\mathrm{2}} \\ $$$${x}^{\mathrm{500}} +\frac{\mathrm{1}}{{x}^{\mathrm{500}} }=\omega^{\mathrm{500}} +\frac{\mathrm{1}}{\omega^{\mathrm{500}} } \\ $$$$\left(\omega^{\mathrm{3}} \right)^{\mathrm{166}} .\omega^{\mathrm{2}} +\frac{\mathrm{1}}{\left(\omega^{\mathrm{3}} \right)^{\mathrm{166}} .\omega^{\mathrm{2}} } \\ $$$$=\omega^{\mathrm{2}} +\frac{\mathrm{1}}{\omega^{\mathrm{2}} }×\frac{\omega}{\omega}=\omega^{\mathrm{2}} +\frac{\omega}{\omega^{\mathrm{3}} }=\omega^{\mathrm{2}} +\omega=−\mathrm{1} \\ $$
Commented by I want to learn more last updated on 17/Aug/20
Thanks sir
$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Answered by floor(10²Eta[1]) last updated on 17/Aug/20
x^2 =−(x+1) x^4 =(−(x+1))^2 =x^2 +2x+1=−x−1+2x+1=x x^5 =x^4 .x=x.x=x^2 =−x−1 x^(10) =(−(x+1))^2 =x^2 +2x+1=−x−1+2x+1=x x^(10) =x∴x^(500) =x^(50) =(x^(10) )^5 =x^5 =−x−1=x^2 ⇒x^(500) +(1/x^(500) )=x^2 +(1/x^2 )=((x^4 +1)/x^2 )=((x+1)/(−(x+1)))=−1
$$\mathrm{x}^{\mathrm{2}} =−\left(\mathrm{x}+\mathrm{1}\right) \\ $$$$\mathrm{x}^{\mathrm{4}} =\left(−\left(\mathrm{x}+\mathrm{1}\right)\right)^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}=−\mathrm{x}−\mathrm{1}+\mathrm{2x}+\mathrm{1}=\mathrm{x} \\ $$$$\mathrm{x}^{\mathrm{5}} =\mathrm{x}^{\mathrm{4}} .\mathrm{x}=\mathrm{x}.\mathrm{x}=\mathrm{x}^{\mathrm{2}} =−\mathrm{x}−\mathrm{1} \\ $$$$\mathrm{x}^{\mathrm{10}} =\left(−\left(\mathrm{x}+\mathrm{1}\right)\right)^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}=−\mathrm{x}−\mathrm{1}+\mathrm{2x}+\mathrm{1}=\mathrm{x} \\ $$$$\mathrm{x}^{\mathrm{10}} =\mathrm{x}\therefore\mathrm{x}^{\mathrm{500}} =\mathrm{x}^{\mathrm{50}} =\left(\mathrm{x}^{\mathrm{10}} \right)^{\mathrm{5}} =\mathrm{x}^{\mathrm{5}} =−\mathrm{x}−\mathrm{1}=\mathrm{x}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{500}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{500}} }=\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }=\frac{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }=\frac{\mathrm{x}+\mathrm{1}}{−\left(\mathrm{x}+\mathrm{1}\right)}=−\mathrm{1} \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 17/Aug/20
e^x cellent approach!
$$\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \mathrm{cellent}\:\mathrm{approach}! \\ $$
Commented by I want to learn more last updated on 17/Aug/20
Thanks sir
$$\mathrm{Thanks}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *