Menu Close

Question-108483

Tinku Tara 0 Comments
Pin




Question Number 108483 by I want to learn more last updated on 17/Aug/20
Commented by Rasheed.Sindhi last updated on 17/Aug/20
Commented by Rasheed.Sindhi last updated on 17/Aug/20
Semicircle area with radius a =(1/2)πa^2 White part= 5 sectors with radius a/2 & 2 equilateral triangles with sides a/2 =5×(1/6)π((a/2))^2 +2×((√3)/4)((a/2))^2 ={5×(1/6)π+2×((√3)/4)}((a/2))^2 =(((5π)/6)+((√3)/2))((a^2 /4)) A=Semicircle−white area =(1/2)πa^2 −(((5π)/6)+((√3)/2))((a^2 /4)) =a^2 {(1/2)π−(((5π)/6)+((√3)/2))((1/4))} =a^2 {(1/2)π−(((5π)/(24))+((√3)/8))} =a^2 {(π/2)−((5π)/(24))−((√3)/8)} =a^2 {((12π−5π−3(√3))/(24))} =((7π−3(√3))/(24))a^2
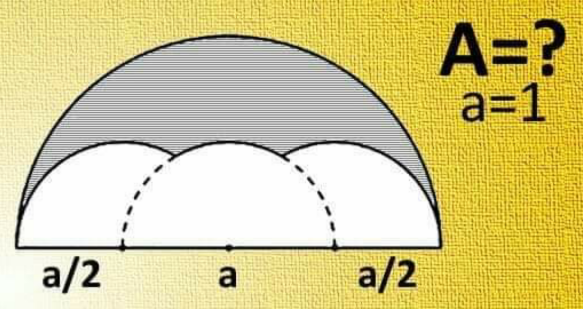
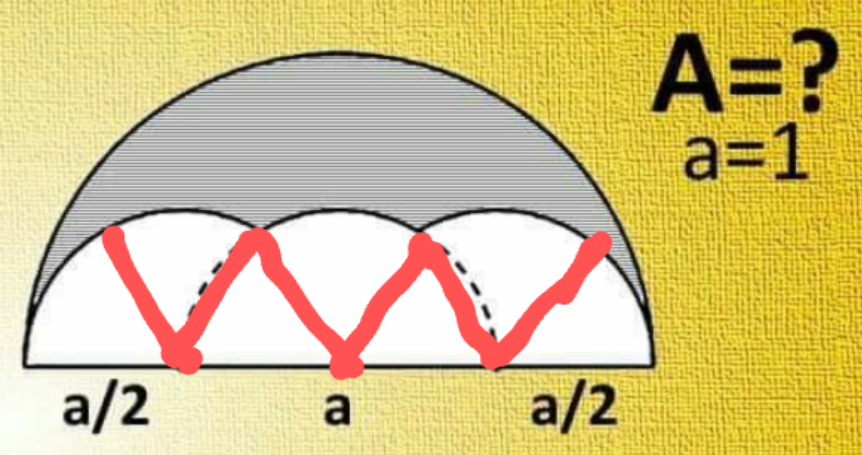
$${Semicircle}\:{area}\:{with}\:{radius}\:{a} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\pi{a}^{\mathrm{2}} \\ $$$${White}\:{part}= \\ $$$$\:\:\:\mathrm{5}\:{sectors}\:{with}\:{radius}\:{a}/\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\& \\ $$$$\:\:\:\mathrm{2}\:{equilateral}\:{triangles}\:{with} \\ $$$$\:\:\:\:{sides}\:{a}/\mathrm{2} \\ $$$$\:\:=\mathrm{5}×\frac{\mathrm{1}}{\mathrm{6}}\pi\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}×\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\:\:=\left\{\mathrm{5}×\frac{\mathrm{1}}{\mathrm{6}}\pi+\mathrm{2}×\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\right\}\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\:\:=\left(\frac{\mathrm{5}\pi}{\mathrm{6}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\left(\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\right) \\ $$$$\mathrm{A}={Semicircle}−{white}\:{area} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\pi{a}^{\mathrm{2}} −\left(\frac{\mathrm{5}\pi}{\mathrm{6}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\left(\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\right) \\ $$$$\:\:\:={a}^{\mathrm{2}} \left\{\frac{\mathrm{1}}{\mathrm{2}}\pi−\left(\frac{\mathrm{5}\pi}{\mathrm{6}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\right\} \\ $$$$\:\:\:={a}^{\mathrm{2}} \left\{\frac{\mathrm{1}}{\mathrm{2}}\pi−\left(\frac{\mathrm{5}\pi}{\mathrm{24}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{8}}\right)\right\} \\ $$$$\:\:\:={a}^{\mathrm{2}} \left\{\frac{\pi}{\mathrm{2}}−\frac{\mathrm{5}\pi}{\mathrm{24}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{8}}\right\} \\ $$$$\:\:\:={a}^{\mathrm{2}} \left\{\frac{\mathrm{12}\pi−\mathrm{5}\pi−\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{24}}\right\} \\ $$$$\:\:\:=\frac{\mathrm{7}\pi−\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{24}}{a}^{\mathrm{2}} \\ $$
Commented by I want to learn more last updated on 17/Aug/20
Thanks sir, i appreciate.
$$\mathrm{Thanks}\:\mathrm{sir},\:\:\mathrm{i}\:\mathrm{appreciate}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *