Question Number 108593 by Rasikh last updated on 18/Aug/20
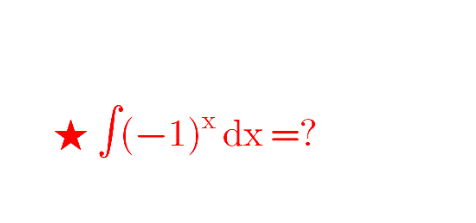
Answered by Her_Majesty last updated on 18/Aug/20
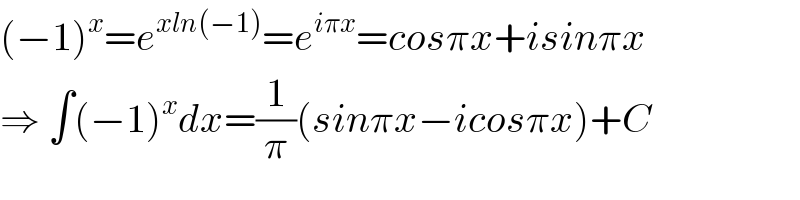
$$\left(−\mathrm{1}\right)^{{x}} ={e}^{{xln}\left(−\mathrm{1}\right)} ={e}^{{i}\pi{x}} ={cos}\pi{x}+{isin}\pi{x} \\ $$$$\Rightarrow\:\int\left(−\mathrm{1}\right)^{{x}} {dx}=\frac{\mathrm{1}}{\pi}\left({sin}\pi{x}−{icos}\pi{x}\right)+{C} \\ $$
