Question Number 108619 by ajfour last updated on 18/Aug/20

Commented by ajfour last updated on 18/Aug/20
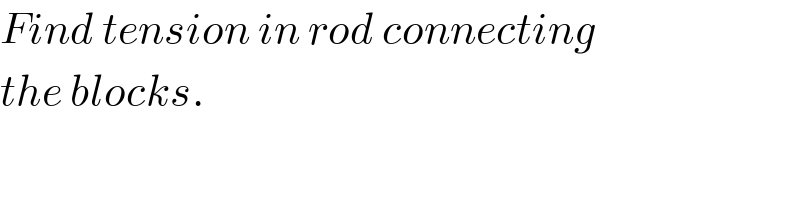
$${Find}\:{tension}\:{in}\:{rod}\:{connecting} \\ $$$${the}\:{blocks}. \\ $$
Commented by Dwaipayan Shikari last updated on 18/Aug/20
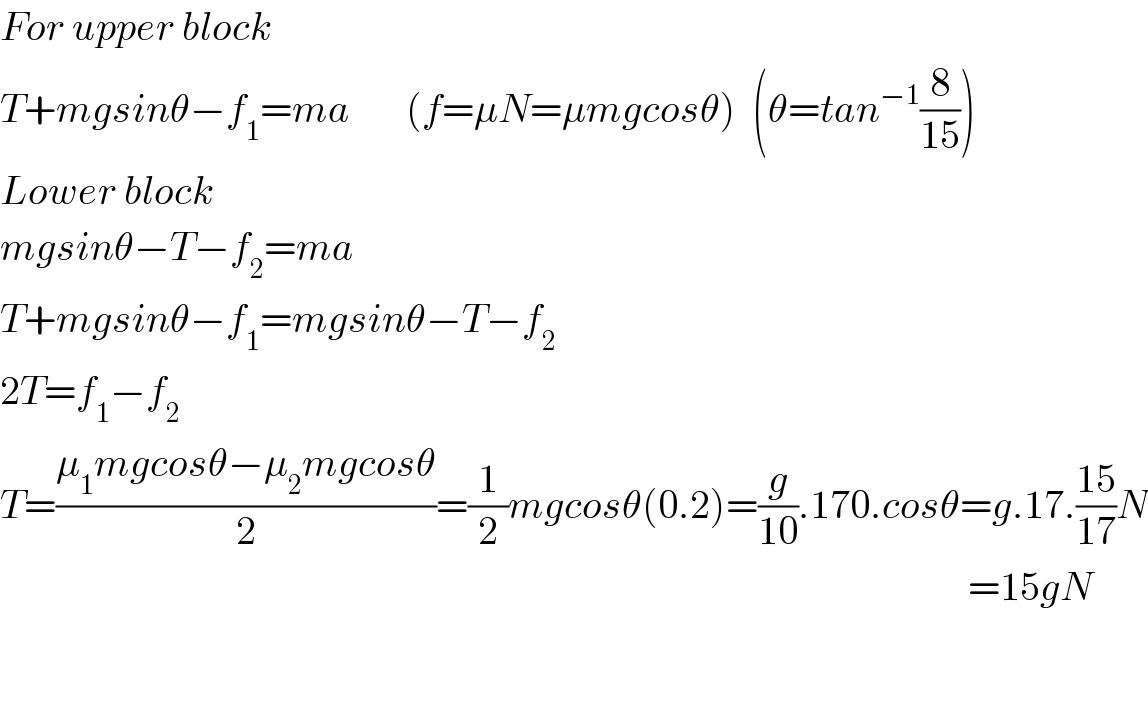
$${For}\:{upper}\:{block} \\ $$$${T}+{mgsin}\theta−{f}_{\mathrm{1}} ={ma}\:\:\:\:\:\:\:\left({f}=\mu{N}=\mu{mgcos}\theta\right)\:\:\left(\theta={tan}^{−\mathrm{1}} \frac{\mathrm{8}}{\mathrm{15}}\right) \\ $$$${Lower}\:{block} \\ $$$${mgsin}\theta−{T}−{f}_{\mathrm{2}} ={ma} \\ $$$${T}+{mgsin}\theta−{f}_{\mathrm{1}} ={mgsin}\theta−{T}−{f}_{\mathrm{2}} \\ $$$$\mathrm{2}{T}={f}_{\mathrm{1}} −{f}_{\mathrm{2}} \\ $$$${T}=\frac{\mu_{\mathrm{1}} {mgcos}\theta−\mu_{\mathrm{2}} {mgcos}\theta}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}{mgcos}\theta\left(\mathrm{0}.\mathrm{2}\right)=\frac{{g}}{\mathrm{10}}.\mathrm{170}.{cos}\theta={g}.\mathrm{17}.\frac{\mathrm{15}}{\mathrm{17}}{N} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{15}{gN} \\ $$$$ \\ $$$$ \\ $$
Commented by ajfour last updated on 18/Aug/20
$${Nice}\:{way},\:{thanks}\:{Sir}. \\ $$
Answered by mr W last updated on 18/Aug/20
![a=acceleration a=((2mg sin θ−mg(μ_1 +μ_2 )cos θ)/(2m)) =[sin θ−(((μ_1 +μ_2 )cos θ)/2)]g >0 T=mg sin θ−μ_2 mg cos θ−ma =mg[sin θ−μ_2 cos θ−((2sin θ−(μ_1 +μ_2 )cos θ)/2)] =((mg(μ_1 −μ_2 )cos θ)/2)](https://www.tinkutara.com/question/Q108627.png)
$${a}={acceleration} \\ $$$${a}=\frac{\mathrm{2}{mg}\:\mathrm{sin}\:\theta−{mg}\left(\mu_{\mathrm{1}} +\mu_{\mathrm{2}} \right)\mathrm{cos}\:\theta}{\mathrm{2}{m}} \\ $$$$=\left[\mathrm{sin}\:\theta−\frac{\left(\mu_{\mathrm{1}} +\mu_{\mathrm{2}} \right)\mathrm{cos}\:\theta}{\mathrm{2}}\right]{g}\:>\mathrm{0} \\ $$$$ \\ $$$${T}={mg}\:\mathrm{sin}\:\theta−\mu_{\mathrm{2}} {mg}\:\mathrm{cos}\:\theta−{ma} \\ $$$$={mg}\left[\mathrm{sin}\:\theta−\mu_{\mathrm{2}} \mathrm{cos}\:\theta−\frac{\mathrm{2sin}\:\theta−\left(\mu_{\mathrm{1}} +\mu_{\mathrm{2}} \right)\mathrm{cos}\:\theta}{\mathrm{2}}\right] \\ $$$$=\frac{{mg}\left(\mu_{\mathrm{1}} −\mu_{\mathrm{2}} \right)\mathrm{cos}\:\theta}{\mathrm{2}} \\ $$
Commented by ajfour last updated on 18/Aug/20
$${Thanks}\:{Sir},\:{right}\:{answer};\:\mathrm{150}{N}. \\ $$
