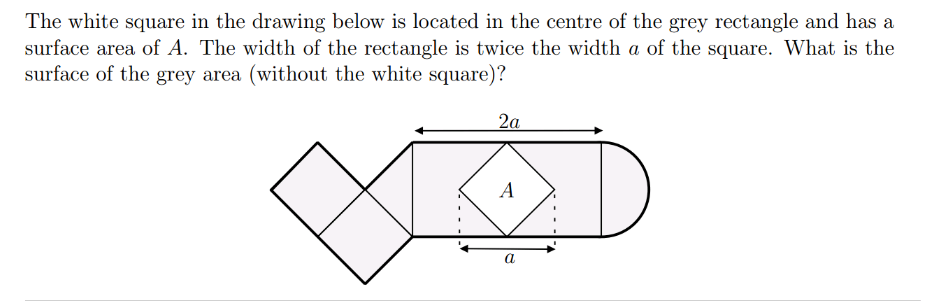
Question Number 108626 by I want to learn more last updated on 18/Aug/20
Answered by Aziztisffola last updated on 18/Aug/20

$$\mathrm{A}_{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{circle}} =\frac{\mathrm{1}}{\mathrm{2}}\pi\left(\frac{\mathrm{a}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\pi\mathrm{a}^{\mathrm{2}} }{\mathrm{8}} \\ $$$$\mathrm{A}_{\mathrm{rectangle}} =\mathrm{2a}^{\mathrm{2}\:} \\ $$$$\mathrm{A}_{\mathrm{triangle}} =\frac{\mathrm{A}}{\mathrm{2}} \\ $$$$\mathrm{A}_{\mathrm{2square}} =\mathrm{2A} \\ $$$$\mathrm{A}_{\mathrm{grey}} =\frac{\pi\mathrm{a}^{\mathrm{2}} }{\mathrm{8}}+\mathrm{2a}^{\mathrm{2}} +\frac{\mathrm{A}}{\mathrm{2}}+\mathrm{2A}−\mathrm{A} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\left(\frac{\mathrm{16}+\pi}{\mathrm{8}}\right)\mathrm{a}^{\mathrm{2}} +\frac{\mathrm{3A}}{\mathrm{2}} \\ $$$$\mathrm{with}\:\mathrm{A}=\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{A}_{\mathrm{grey}} =\left(\frac{\mathrm{16}+\pi}{\mathrm{8}}\right)\mathrm{a}^{\mathrm{2}} +\frac{\mathrm{3a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\left(\frac{\mathrm{22}+\pi}{\mathrm{8}}\right)\mathrm{a}^{\mathrm{2}} \\ $$
Commented by I want to learn more last updated on 18/Aug/20
$$\mathrm{Thanks}\:\mathrm{sir},\:\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$
