Question Number 108637 by mathdave last updated on 18/Aug/20

Answered by bemath last updated on 18/Aug/20
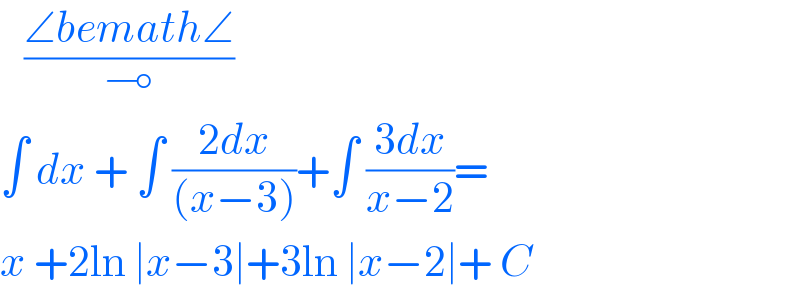
$$\:\:\:\frac{\angle{bemath}\angle}{\multimap} \\ $$$$\int\:{dx}\:+\:\int\:\frac{\mathrm{2}{dx}}{\left({x}−\mathrm{3}\right)}+\int\:\frac{\mathrm{3}{dx}}{{x}−\mathrm{2}}= \\ $$$${x}\:+\mathrm{2ln}\:\mid{x}−\mathrm{3}\mid+\mathrm{3ln}\:\mid{x}−\mathrm{2}\mid+\:{C} \\ $$
Answered by mathmax by abdo last updated on 18/Aug/20
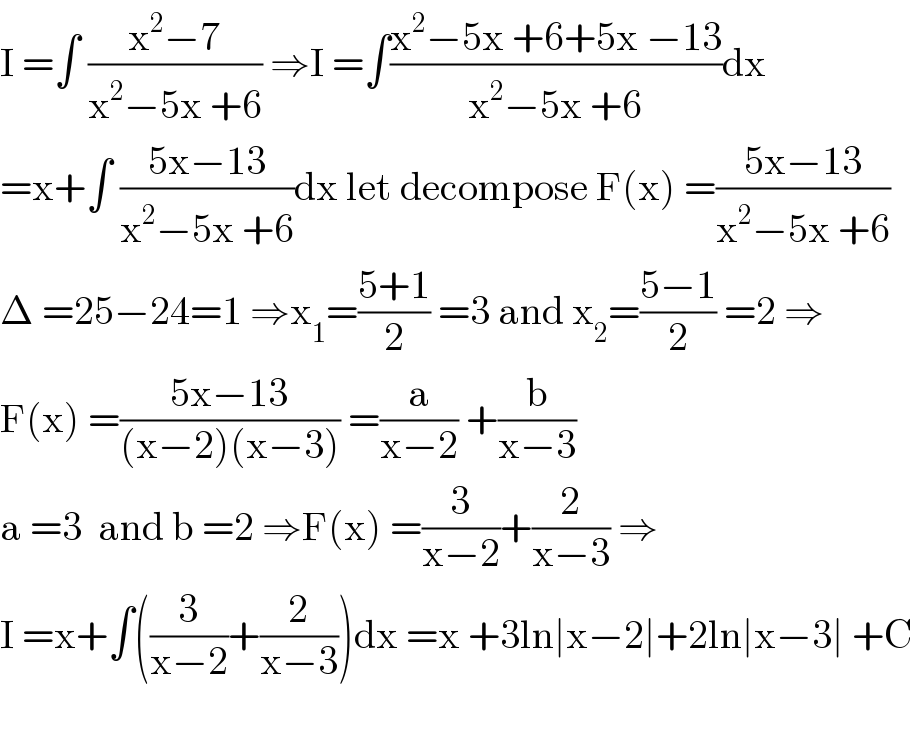
$$\mathrm{I}\:=\int\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{7}}{\mathrm{x}^{\mathrm{2}} −\mathrm{5x}\:+\mathrm{6}}\:\Rightarrow\mathrm{I}\:=\int\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{5x}\:+\mathrm{6}+\mathrm{5x}\:−\mathrm{13}}{\mathrm{x}^{\mathrm{2}} −\mathrm{5x}\:+\mathrm{6}}\mathrm{dx} \\ $$$$=\mathrm{x}+\int\:\frac{\mathrm{5x}−\mathrm{13}}{\mathrm{x}^{\mathrm{2}} −\mathrm{5x}\:+\mathrm{6}}\mathrm{dx}\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{5x}−\mathrm{13}}{\mathrm{x}^{\mathrm{2}} −\mathrm{5x}\:+\mathrm{6}} \\ $$$$\Delta\:=\mathrm{25}−\mathrm{24}=\mathrm{1}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =\frac{\mathrm{5}+\mathrm{1}}{\mathrm{2}}\:=\mathrm{3}\:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} =\frac{\mathrm{5}−\mathrm{1}}{\mathrm{2}}\:=\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{5x}−\mathrm{13}}{\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}−\mathrm{3}\right)}\:=\frac{\mathrm{a}}{\mathrm{x}−\mathrm{2}}\:+\frac{\mathrm{b}}{\mathrm{x}−\mathrm{3}} \\ $$$$\mathrm{a}\:=\mathrm{3}\:\:\mathrm{and}\:\mathrm{b}\:=\mathrm{2}\:\Rightarrow\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{3}}{\mathrm{x}−\mathrm{2}}+\frac{\mathrm{2}}{\mathrm{x}−\mathrm{3}}\:\Rightarrow \\ $$$$\mathrm{I}\:=\mathrm{x}+\int\left(\frac{\mathrm{3}}{\mathrm{x}−\mathrm{2}}+\frac{\mathrm{2}}{\mathrm{x}−\mathrm{3}}\right)\mathrm{dx}\:=\mathrm{x}\:+\mathrm{3ln}\mid\mathrm{x}−\mathrm{2}\mid+\mathrm{2ln}\mid\mathrm{x}−\mathrm{3}\mid\:+\mathrm{C} \\ $$$$ \\ $$
