Question Number 108643 by ajfour last updated on 18/Aug/20
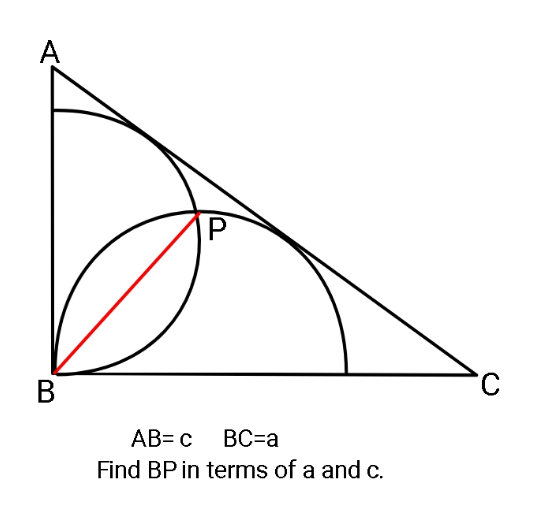
Answered by mr W last updated on 18/Aug/20

Commented by mr W last updated on 18/Aug/20
![(r/(AD))=((BC)/(AC))=(a/( (√(a^2 +c^2 )))) (r/(c−r))=(a/( (√(a^2 +c^2 )))) ⇒r=((ac)/( a+(√(a^2 +c^2 )))) similarly ⇒R=((ac)/( c+(√(a^2 +c^2 )))) cos ∠DBP=((BP)/(2r)) cos ∠EBP=((BP)/(2R))=sin ∠DBP ((BP^2 )/4)((1/r^2 )+(1/R^2 ))=1 BP^2 [(a+(√(a^2 +c^2 )))^2 +(c+(√(a^2 +c^2 )))^2 ]=4a^2 c^2 BP^2 [3a^2 +3c^2 +2(a+c)(√(a^2 +c^2 ))]=4a^2 c^2 ⇒BP=((2ac)/( (√(3(a^2 +c^2 )+2(a+c)(√(a^2 +c^2 ))))))](https://www.tinkutara.com/question/Q108724.png)
$$\frac{{r}}{{AD}}=\frac{{BC}}{{AC}}=\frac{{a}}{\:\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }} \\ $$$$\frac{{r}}{{c}−{r}}=\frac{{a}}{\:\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }} \\ $$$$\Rightarrow{r}=\frac{{ac}}{\:{a}+\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }} \\ $$$${similarly} \\ $$$$\Rightarrow{R}=\frac{{ac}}{\:{c}+\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }} \\ $$$$\mathrm{cos}\:\angle{DBP}=\frac{{BP}}{\mathrm{2}{r}} \\ $$$$\mathrm{cos}\:\angle{EBP}=\frac{{BP}}{\mathrm{2}{R}}=\mathrm{sin}\:\angle{DBP} \\ $$$$\frac{{BP}^{\mathrm{2}} }{\mathrm{4}}\left(\frac{\mathrm{1}}{{r}^{\mathrm{2}} }+\frac{\mathrm{1}}{{R}^{\mathrm{2}} }\right)=\mathrm{1} \\ $$$${BP}^{\mathrm{2}} \left[\left({a}+\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }\right)^{\mathrm{2}} +\left({c}+\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }\right)^{\mathrm{2}} \right]=\mathrm{4}{a}^{\mathrm{2}} {c}^{\mathrm{2}} \\ $$$${BP}^{\mathrm{2}} \left[\mathrm{3}{a}^{\mathrm{2}} +\mathrm{3}{c}^{\mathrm{2}} +\mathrm{2}\left({a}+{c}\right)\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }\right]=\mathrm{4}{a}^{\mathrm{2}} {c}^{\mathrm{2}} \\ $$$$\Rightarrow{BP}=\frac{\mathrm{2}{ac}}{\:\sqrt{\mathrm{3}\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)+\mathrm{2}\left({a}+{c}\right)\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }}} \\ $$
Commented by ajfour last updated on 18/Aug/20
$$\:\:\:\:\:\:\:\mathcal{A}{wesome}!\:{Great}\:{work}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{thanks}\:{a}\:{lot}\:{Sir}. \\ $$
Answered by ajfour last updated on 19/Aug/20
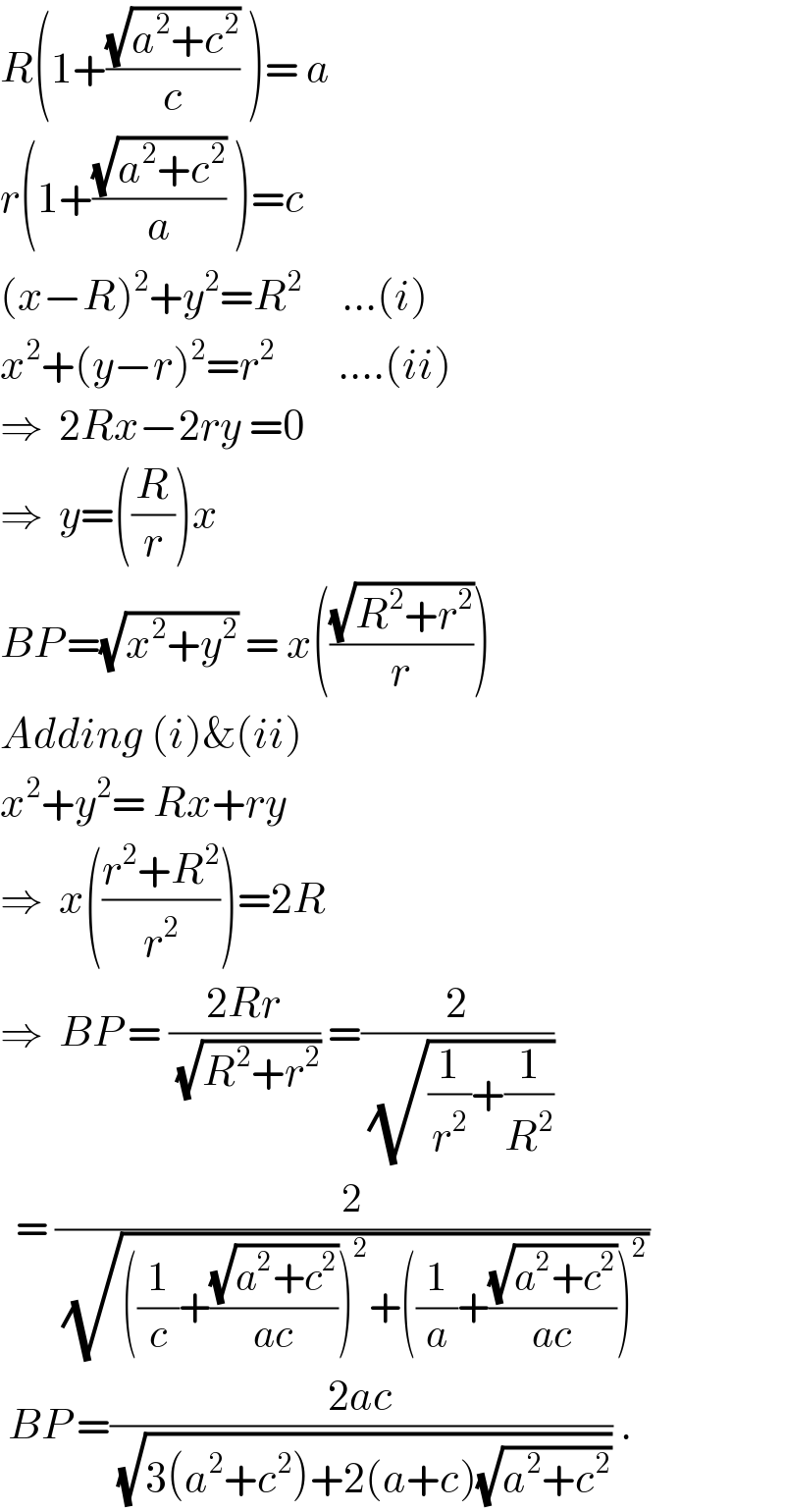
$${R}\left(\mathrm{1}+\frac{\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }}{{c}}\:\right)=\:{a} \\ $$$${r}\left(\mathrm{1}+\frac{\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }}{{a}}\:\right)={c} \\ $$$$\left({x}−{R}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={R}^{\mathrm{2}} \:\:\:\:\:…\left({i}\right) \\ $$$${x}^{\mathrm{2}} +\left({y}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \:\:\:\:\:\:\:\:….\left({ii}\right) \\ $$$$\Rightarrow\:\:\mathrm{2}{Rx}−\mathrm{2}{ry}\:=\mathrm{0} \\ $$$$\Rightarrow\:\:{y}=\left(\frac{{R}}{{r}}\right){x} \\ $$$${BP}^{\:} =\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:=\:{x}\left(\frac{\sqrt{{R}^{\mathrm{2}} +{r}^{\mathrm{2}} }}{{r}}\right) \\ $$$${Adding}\:\left({i}\right)\&\left({ii}\right) \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\:{Rx}+{ry} \\ $$$$\Rightarrow\:\:{x}\left(\frac{{r}^{\mathrm{2}} +{R}^{\mathrm{2}} }{{r}^{\mathrm{2}} }\right)=\mathrm{2}{R} \\ $$$$\Rightarrow\:\:{BP}\:=\:\frac{\mathrm{2}{Rr}}{\:\sqrt{{R}^{\mathrm{2}} +{r}^{\mathrm{2}} }}\:=\frac{\mathrm{2}}{\:\sqrt{\frac{\mathrm{1}}{{r}^{\mathrm{2}} }+\frac{\mathrm{1}}{{R}^{\mathrm{2}} }}} \\ $$$$\:\:=\:\frac{\mathrm{2}}{\:\sqrt{\left(\frac{\mathrm{1}}{{c}}+\frac{\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }}{{ac}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{{a}}+\frac{\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }}{{ac}}\right)^{\mathrm{2}} }} \\ $$$$\:{BP}\:=\frac{\mathrm{2}{ac}}{\:\sqrt{\mathrm{3}\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)+\mathrm{2}\left({a}+{c}\right)\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }}}\:. \\ $$
