Question Number 108663 by bobhans last updated on 18/Aug/20

Answered by john santu last updated on 18/Aug/20
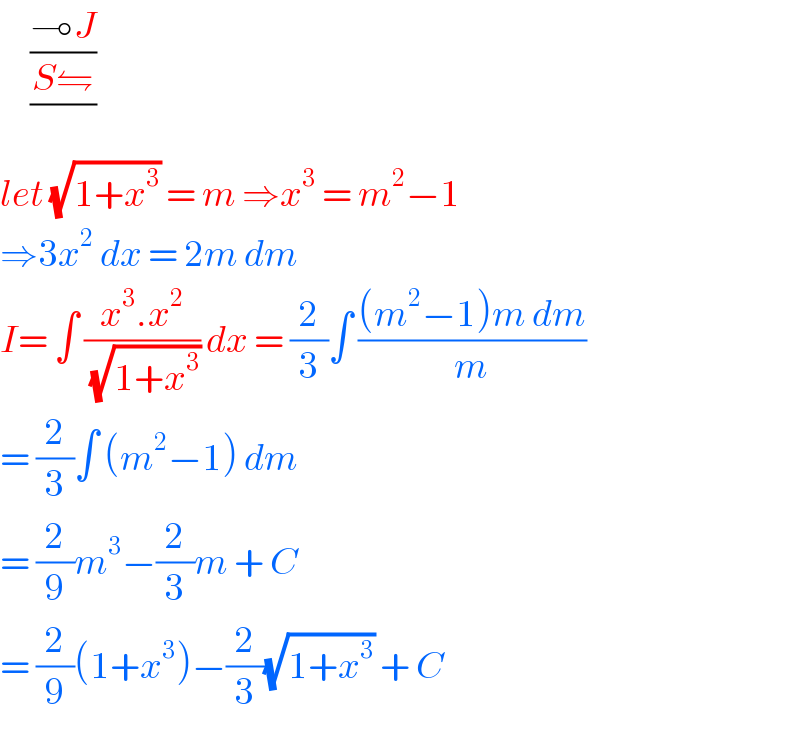
$$\:\:\:\:\:\frac{\frac{\multimap{J}}{{S}\leftrightharpoons}}{} \\ $$$${let}\:\sqrt{\mathrm{1}+{x}^{\mathrm{3}} }\:=\:{m}\:\Rightarrow{x}^{\mathrm{3}} \:=\:{m}^{\mathrm{2}} −\mathrm{1} \\ $$$$\Rightarrow\mathrm{3}{x}^{\mathrm{2}} \:{dx}\:=\:\mathrm{2}{m}\:{dm} \\ $$$${I}=\:\int\:\frac{{x}^{\mathrm{3}} .{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}+{x}^{\mathrm{3}} }}\:{dx}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\int\:\frac{\left({m}^{\mathrm{2}} −\mathrm{1}\right){m}\:{dm}}{{m}} \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{3}}\int\:\left({m}^{\mathrm{2}} −\mathrm{1}\right)\:{dm}\: \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{9}}{m}^{\mathrm{3}} −\frac{\mathrm{2}}{\mathrm{3}}{m}\:+\:{C} \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{9}}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)−\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\mathrm{1}+{x}^{\mathrm{3}} }\:+\:{C} \\ $$
