Question Number 108667 by bobhans last updated on 18/Aug/20

Answered by john santu last updated on 18/Aug/20

Commented by john santu last updated on 18/Aug/20
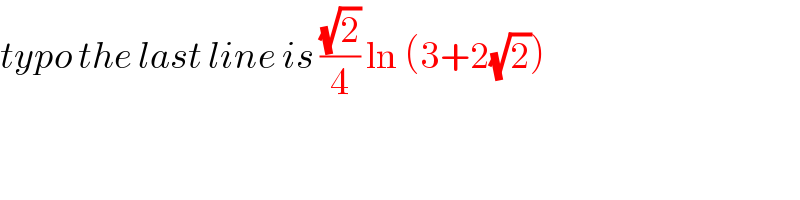
$${typo}\:{the}\:{last}\:{line}\:{is}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\:\mathrm{ln}\:\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)\: \\ $$
Commented by bobhans last updated on 18/Aug/20

$${yes}….{right} \\ $$
Answered by ajfour last updated on 18/Aug/20
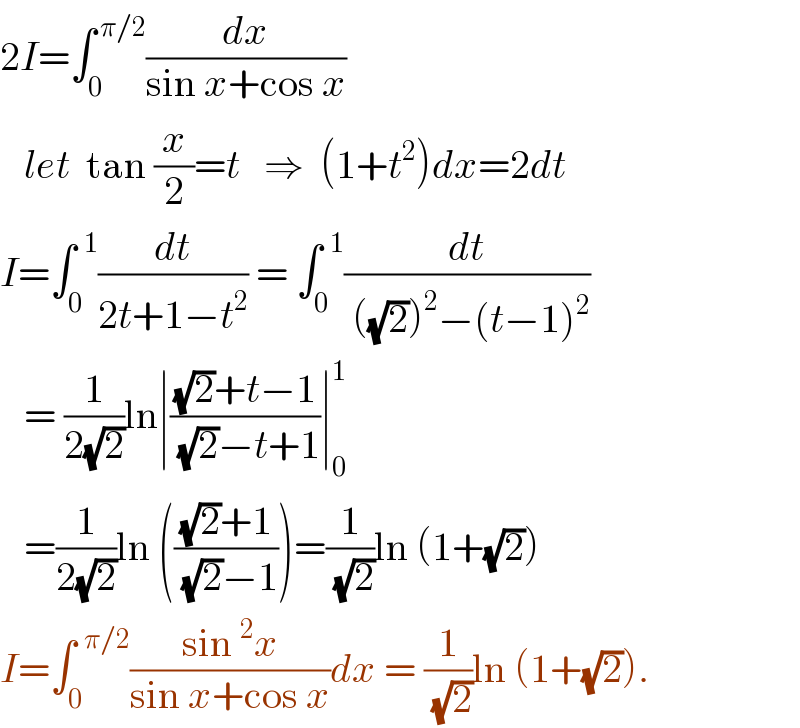
$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \frac{{dx}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}} \\ $$$$\:\:\:{let}\:\:\mathrm{tan}\:\frac{{x}}{\mathrm{2}}={t}\:\:\:\Rightarrow\:\:\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dx}=\mathrm{2}{dt} \\ $$$${I}=\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{{dt}}{\mathrm{2}{t}+\mathrm{1}−{t}^{\mathrm{2}} }\:=\:\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{{dt}}{\:\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} −\left({t}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\sqrt{\mathrm{2}}+{t}−\mathrm{1}}{\:\sqrt{\mathrm{2}}−{t}+\mathrm{1}}\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\:\left(\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\: \\ $$$${I}=\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} \frac{\mathrm{sin}\:^{\mathrm{2}} {x}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{dx}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right). \\ $$
Commented by bobhans last updated on 18/Aug/20
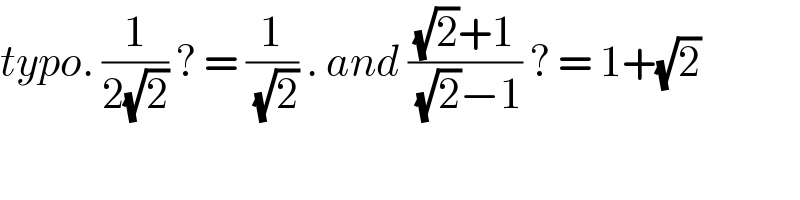
$${typo}.\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:?\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:.\:{and}\:\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\:?\:=\:\mathrm{1}+\sqrt{\mathrm{2}}\: \\ $$
Commented by ajfour last updated on 18/Aug/20
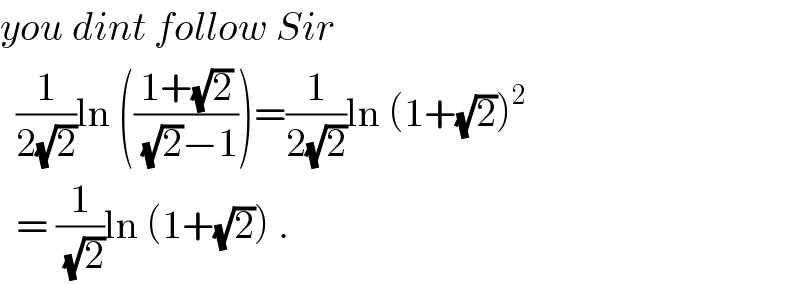
$${you}\:{dint}\:{follow}\:{Sir} \\ $$$$\:\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\:\left(\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\right)=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\:\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\:. \\ $$
Answered by mathmax by abdo last updated on 18/Aug/20
![I =∫_0 ^(π/2) ((sin^2 x)/(sinx +cosx))dx and J =∫_0 ^(π/2) ((cos^2 x)/(sinx +cosx))dx( friend of I) ⇒I−J =∫_0 ^(π/2) ((sin^2 x −cos^2 x)/(sinx +cosx))dx =∫_0 ^(π/2) (sinx −cosx)dx =[−cosx −sinx]_0 ^(π/2) =−1+1 =0 ⇒I =J I +J =2I =∫_0 ^(π/2) (dx/(cosx +sinx)) =_(tan((x/2))=t) ∫_0 ^1 ((2dt)/((1+t^2 )(((1−t^2 )/(1+t^2 ))+((2t)/(1+t^2 ))))) =2 ∫_0 ^1 (dt/(1−t^2 +2t)) =−2 ∫_0 ^1 (dt/(t^2 −2t−1)) Δ^′ =1+1 =2 ⇒t_1 =1+(√2) and t_2 =1−(√2) ⇒ I =− ∫_0 ^1 (dt/((t−t_1 )(t−t_2 ))) =−(1/(2(√2)))∫_0 ^1 ((1/(t−t_1 ))−(1/(t−t_2 )))dt =(1/(2(√2)))[ln∣((t−t_2 )/(t−t_1 ))∣]_0 ^1 =(1/(2(√2)))[ln∣((t−1+(√2))/(t−1−(√2)))∣]_0 ^1 =(1/(2(√2))){−ln∣((−1+(√2))/(−1−(√2)))∣} =−(1/(2(√2)))ln((((√2)−1)/( (√2)+1))) =(1/(2(√2)))ln((((√2)+1)/( (√2)−1)))](https://www.tinkutara.com/question/Q108681.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{sinx}\:+\mathrm{cosx}}\mathrm{dx}\:\:\mathrm{and}\:\mathrm{J}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{sinx}\:+\mathrm{cosx}}\mathrm{dx}\left(\:\mathrm{friend}\:\mathrm{of}\:\mathrm{I}\right) \\ $$$$\Rightarrow\mathrm{I}−\mathrm{J}\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}\:−\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{sinx}\:+\mathrm{cosx}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{sinx}\:−\mathrm{cosx}\right)\mathrm{dx} \\ $$$$=\left[−\mathrm{cosx}\:−\mathrm{sinx}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=−\mathrm{1}+\mathrm{1}\:=\mathrm{0}\:\Rightarrow\mathrm{I}\:=\mathrm{J} \\ $$$$\mathrm{I}\:+\mathrm{J}\:=\mathrm{2I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dx}}{\mathrm{cosx}\:+\mathrm{sinx}}\:=_{\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{t}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }+\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{1}−\mathrm{t}^{\mathrm{2}} \:+\mathrm{2t}}\:=−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{2t}−\mathrm{1}} \\ $$$$\Delta^{'} \:=\mathrm{1}+\mathrm{1}\:=\mathrm{2}\:\Rightarrow\mathrm{t}_{\mathrm{1}} =\mathrm{1}+\sqrt{\mathrm{2}}\:\mathrm{and}\:\mathrm{t}_{\mathrm{2}} =\mathrm{1}−\sqrt{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{I}\:=−\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\left(\mathrm{t}−\mathrm{t}_{\mathrm{1}} \right)\left(\mathrm{t}−\mathrm{t}_{\mathrm{2}} \right)}\:=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\frac{\mathrm{1}}{\mathrm{t}−\mathrm{t}_{\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{t}−\mathrm{t}_{\mathrm{2}} }\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left[\mathrm{ln}\mid\frac{\mathrm{t}−\mathrm{t}_{\mathrm{2}} }{\mathrm{t}−\mathrm{t}_{\mathrm{1}} }\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left[\mathrm{ln}\mid\frac{\mathrm{t}−\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{t}−\mathrm{1}−\sqrt{\mathrm{2}}}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \: \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{−\mathrm{ln}\mid\frac{−\mathrm{1}+\sqrt{\mathrm{2}}}{−\mathrm{1}−\sqrt{\mathrm{2}}}\mid\right\}\:=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\left(\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}\right)\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\left(\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\right) \\ $$$$ \\ $$
Answered by 1549442205PVT last updated on 18/Aug/20
![Set J=∫_0 ^(π/2) ((cos^2 x)/(sinx+cosx))dx and t=(π/2)−x ⇒dx=−dt⇒ I=∫_0 ^(π/2) ((sin^2 x)/(sinx+cosx))dx =∫_(π/2) ^0 ((cos^2 t)/(sint+cost))(−1)dt=∫_0 ^(π/2) ((cos^2 t)/(sint+cost))dt=J ⇒2I=I+J=∫_0 ^(π/2) (dx/(cosx+sinx)) =∫_0 ^(π/2) ((cosx+sins)/((sinx+cosx)^2 ))dx = ∫_0 ^(π/2) (((√2)sin(x+(π/4)))/([(√2)sin(x+(π/4))]^2 ))dx =−(1/( (√2))) ∫_0 ^(π/2) ((d[cos(x+(π/4))])/(1−cos^2 (x+(π/4))))dx Set cos(x+(π/4))=u⇒u∣_(1/(√2)) ^(−1/(√2)) =(1/( (√2))) ∫_0 ^(π/2) (du/(u^2 −1))dx=(1/( 2(√2)))∫_0 ^(π/2) ((1/(u−1))−(1/(1+u)))du =(1/(2(√2)))(ln∣u−1∣−ln∣u+1∣)∣_(1/(√2)) ^(−1/(√2)) ==(1/(2(√2)))ln∣((u−1)/(u+1))∣∣_(1/(√2)) ^(−1/(√2)) =(1/( 2(√2)))(ln∣(((√(2+))1)/( (√2)−1))∣−ln(((√2)−1)/( (√2)+1))) =(1/(2(√2)))ln((((√2)+1)^2 )/(((√2)−1)^2 ))=(1/( (√2)))ln(((√2)+1)/( (√2)−1))=(√2)ln((√2)+1) ⇒I=(1/( (√2)))ln((√2)+1)](https://www.tinkutara.com/question/Q108696.png)
$$\mathrm{Set}\:\mathrm{J}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{sinx}+\mathrm{cosx}}\mathrm{dx}\:\mathrm{and}\:\mathrm{t}=\frac{\pi}{\mathrm{2}}−\mathrm{x} \\ $$$$\Rightarrow\mathrm{dx}=−\mathrm{dt}\Rightarrow\:\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{sinx}+\mathrm{cosx}}\mathrm{dx}\: \\ $$$$=\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} \frac{\mathrm{cos}^{\mathrm{2}} \mathrm{t}}{\mathrm{sint}+\mathrm{cost}}\left(−\mathrm{1}\right)\mathrm{dt}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cos}^{\mathrm{2}} \mathrm{t}}{\mathrm{sint}+\mathrm{cost}}\mathrm{dt}=\mathrm{J} \\ $$$$\Rightarrow\mathrm{2I}=\mathrm{I}+\mathrm{J}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{dx}}{\mathrm{cosx}+\mathrm{sinx}} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cosx}+\mathrm{sins}}{\left(\mathrm{sinx}+\mathrm{cosx}\right)^{\mathrm{2}} }\mathrm{dx}\: \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\sqrt{\mathrm{2}}\mathrm{sin}\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)}{\left[\sqrt{\mathrm{2}}\mathrm{sin}\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)\right]^{\mathrm{2}} }\mathrm{dx}\: \\ $$$$=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{\mathrm{d}\left[\mathrm{cos}\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)\right]}{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)}\mathrm{dx}\: \\ $$$$\mathrm{Set}\:\mathrm{cos}\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)=\mathrm{u}\Rightarrow\mathrm{u}\mid_{\mathrm{1}/\sqrt{\mathrm{2}}} ^{−\mathrm{1}/\sqrt{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\mathrm{dx}=\frac{\mathrm{1}}{\:\mathrm{2}\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\mathrm{1}}{\mathrm{u}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}}\right)\mathrm{du}\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left(\mathrm{ln}\mid\mathrm{u}−\mathrm{1}\mid−\mathrm{ln}\mid\mathrm{u}+\mathrm{1}\mid\right)\mid_{\mathrm{1}/\sqrt{\mathrm{2}}} ^{−\mathrm{1}/\sqrt{\mathrm{2}}} \\ $$$$==\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\mathrm{u}−\mathrm{1}}{\mathrm{u}+\mathrm{1}}\mid\mid_{\mathrm{1}/\sqrt{\mathrm{2}}} ^{−\mathrm{1}/\sqrt{\mathrm{2}}} =\frac{\mathrm{1}}{\:\mathrm{2}\sqrt{\mathrm{2}}}\left(\mathrm{ln}\mid\frac{\sqrt{\mathrm{2}+}\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\mid−\mathrm{ln}\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}\right) \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\frac{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} }{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{ln}\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}=\sqrt{\mathrm{2}}\mathrm{ln}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{I}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{ln}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right) \\ $$
