Question Number 108780 by 150505R last updated on 19/Aug/20

Answered by bobhans last updated on 19/Aug/20
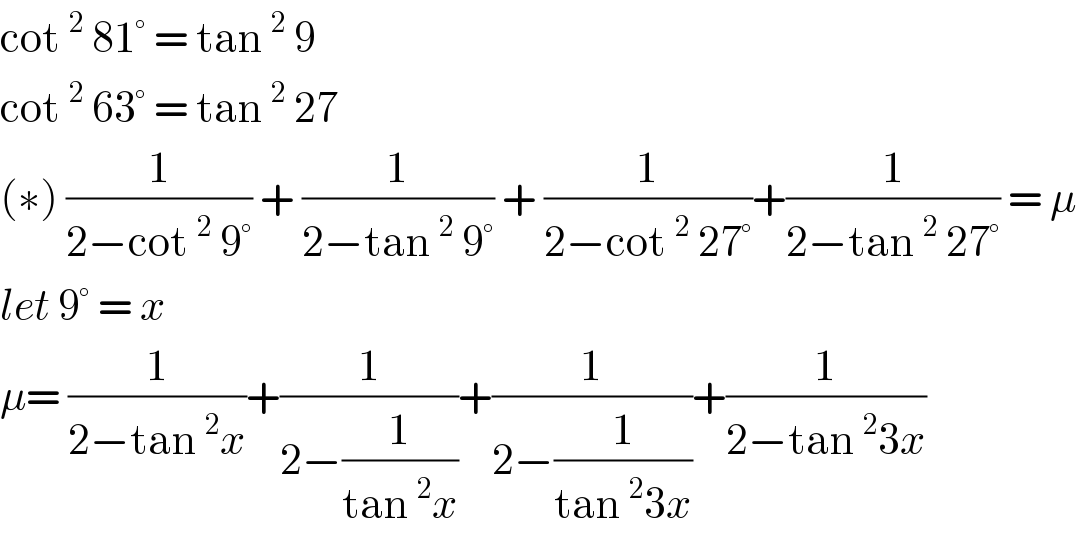
$$\mathrm{cot}\:^{\mathrm{2}} \:\mathrm{81}°\:=\:\mathrm{tan}\:^{\mathrm{2}} \:\mathrm{9}\: \\ $$$$\mathrm{cot}\:^{\mathrm{2}} \:\mathrm{63}°\:=\:\mathrm{tan}\:^{\mathrm{2}} \:\mathrm{27}\: \\ $$$$\left(\ast\right)\:\frac{\mathrm{1}}{\mathrm{2}−\mathrm{cot}\:^{\mathrm{2}} \:\mathrm{9}°}\:+\:\frac{\mathrm{1}}{\mathrm{2}−\mathrm{tan}\:^{\mathrm{2}} \:\mathrm{9}°}\:+\:\frac{\mathrm{1}}{\mathrm{2}−\mathrm{cot}\:^{\mathrm{2}} \:\mathrm{27}°}+\frac{\mathrm{1}}{\mathrm{2}−\mathrm{tan}\:^{\mathrm{2}} \:\mathrm{27}°}\:=\:\mu \\ $$$${let}\:\mathrm{9}°\:=\:{x}\: \\ $$$$\mu=\:\frac{\mathrm{1}}{\mathrm{2}−\mathrm{tan}\:^{\mathrm{2}} {x}}+\frac{\mathrm{1}}{\mathrm{2}−\frac{\mathrm{1}}{\mathrm{tan}\:^{\mathrm{2}} {x}}}+\frac{\mathrm{1}}{\mathrm{2}−\frac{\mathrm{1}}{\mathrm{tan}\:^{\mathrm{2}} \mathrm{3}{x}}}+\frac{\mathrm{1}}{\mathrm{2}−\mathrm{tan}\:^{\mathrm{2}} \mathrm{3}{x}} \\ $$
Commented by bobhans last updated on 19/Aug/20

$${let}\:\mathrm{tan}\:{x}\:=\:{q}\: \\ $$$$ \\ $$
Commented by 150505R last updated on 19/Aug/20
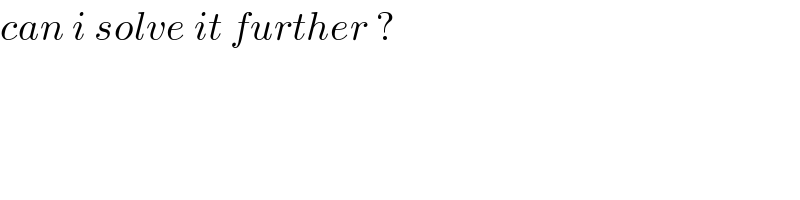
$${can}\:{i}\:{solve}\:{it}\:{further}\:? \\ $$
