Question Number 108839 by 150505R last updated on 19/Aug/20
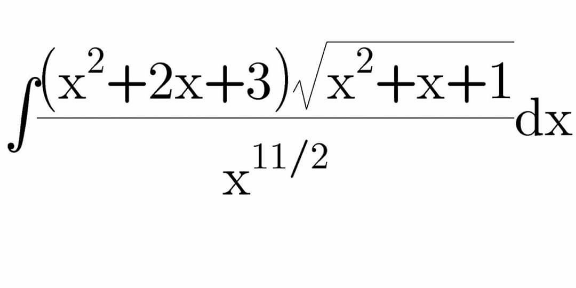
Commented by Her_Majesty last updated on 20/Aug/20
![this looks to me as if the integral must be ((p(x^2 +x+1)^(3/2) )/x^q ) with p, q ∈Q (d/dx)[(((x^2 +x+1)^(3/2) p)/x^q )]=−((p(2(q−3)x^2 +(2q−3)x+2q)(√(x^2 +x+1)))/x^(q+1) ) ⇒ q=9/2 −((3p(x^2 +2x+3)(√(x^2 +x+1)))/(2x^(11/2) )) ⇒ p=−2/3 ⇒ ∫(((x^2 +2x+3)(√(x^2 +x+1)))/x^(11/2) )dx=−((2(x^2 +x+1)^(3/2) )/(3x^(9/2) ))+C](https://www.tinkutara.com/question/Q108887.png)
$${this}\:{looks}\:{to}\:{me}\:{as}\:{if}\:{the}\:{integral}\:{must}\:{be} \\ $$$$\frac{{p}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} }{{x}^{{q}} }\:{with}\:{p},\:{q}\:\in\mathbb{Q} \\ $$$$\frac{{d}}{{dx}}\left[\frac{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} {p}}{{x}^{{q}} }\right]=−\frac{{p}\left(\mathrm{2}\left({q}−\mathrm{3}\right){x}^{\mathrm{2}} +\left(\mathrm{2}{q}−\mathrm{3}\right){x}+\mathrm{2}{q}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{{x}^{{q}+\mathrm{1}} } \\ $$$$\Rightarrow\:{q}=\mathrm{9}/\mathrm{2} \\ $$$$−\frac{\mathrm{3}{p}\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{\mathrm{2}{x}^{\mathrm{11}/\mathrm{2}} } \\ $$$$\Rightarrow\:{p}=−\mathrm{2}/\mathrm{3} \\ $$$$\Rightarrow \\ $$$$\int\frac{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{{x}^{\mathrm{11}/\mathrm{2}} }{dx}=−\frac{\mathrm{2}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} }{\mathrm{3}{x}^{\mathrm{9}/\mathrm{2}} }+{C} \\ $$
